A semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.
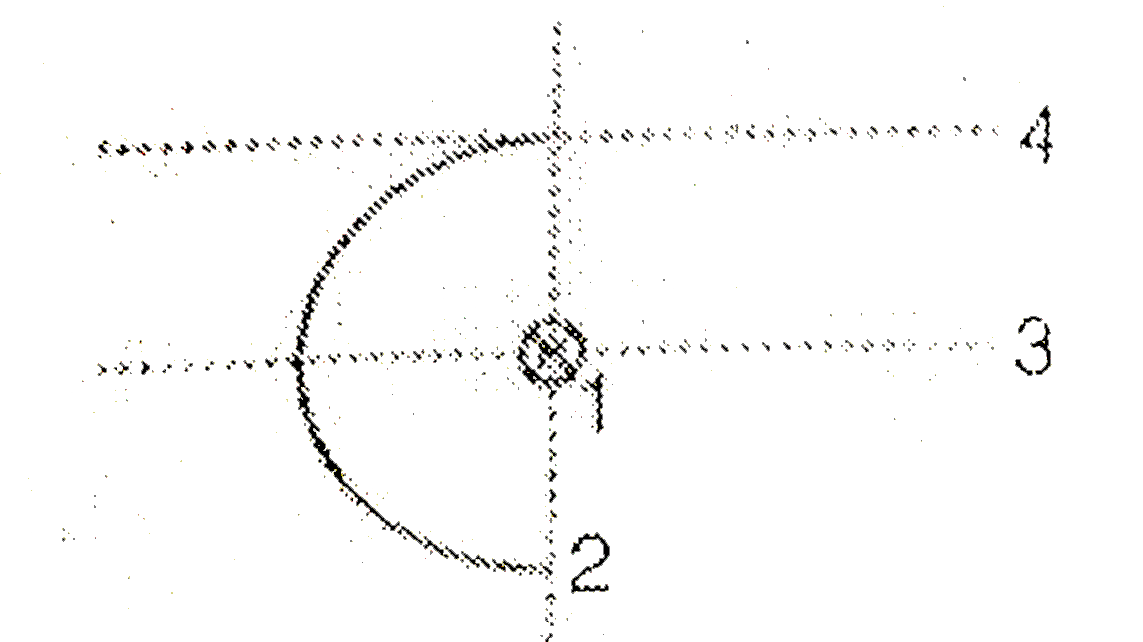

The correct Answer is:(A)R,(B)P,(C)P,(D)Q
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
41 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A semicircular ring has mass m and radius R as shown in figure. Let I1,I2,I3andI4 be the moments of inertia of the four axes as shown. Axis 1 passes through centre and is perpendicular to plane of ring. Then, match the following columns.

Column-IColumn-II(A)I1(p)mR22(B)I2(q)(3/2)mR2(C)I3(r)mR2(D)I4(s)Data is insufficient
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution
Knowledge Check
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2The moment of inertia of a thin uniform ring of mass I kg about an axis passing through the centre and perpendicular to the plane of the ring is 0.25 kg m2. Then the diameter of the ring is
A0.25mB0.5mC0.75mD1mThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
A2 mB4 mC5 mD6 m
Derive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
View SolutionFrom a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View SolutionFrom a complete ring of mass M and radius R, a 30∘sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View SolutionConsider a semicircular ring with mass m and radius R as shown in figure.
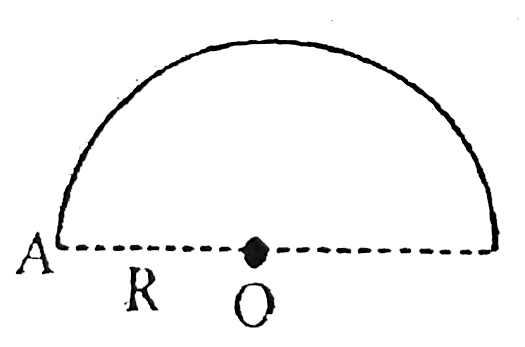
Statement-1: The moment of inertia of semi - circular ring about an axis passing through A and perpendicular to plane is 2mR2
Statement-2: According to parallel axis theorem: IA=1cm+mR2
View Solution
