There are two point masses A and B, situated at origin and point (5m,0m) respectively . At a certain time $v_{A}$ and $v_{B}$ are respectively the velocities of point masses A and B . Match the situations under Table-1 with their correct option under Table-2

Text Solution

Verified by Experts

The correct Answer is:(A)P,(B)S,(C)Q,(D)R

Updated on:21/07/2023

Two point charges $- q$ and $+ q / 2$ are situated at the origin and the point $(a, 0, 0)$ respectively. The point along the $X$ -axis where the electric field Vanishes is
A $x = \frac{a}{\sqrt{2}}$
B $x = \sqrt{2} a$
C $x = \frac{\sqrt{2} a}{\sqrt{2} - 1}$
D $x = \frac{\sqrt{2} a}{\sqrt{2} + 1}$
Two particles $A and B$ of masses $m_{A} and m_{B}$ respectively and having the same charge are moving in a plane . The speeds of the particles are $v_{A} and v_{B}$ respectively and the trajectories are as shown in the figure. Then

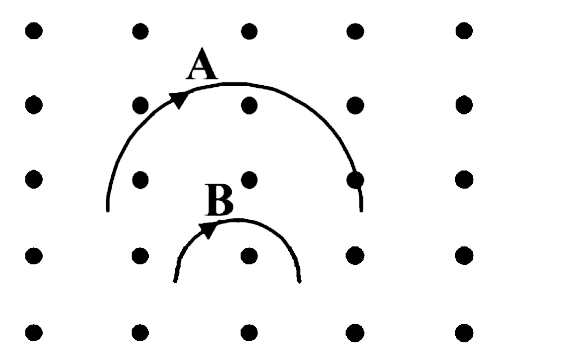A $m_{A} v_{A} < m_{B} v_{B}$
B $m_{A} v_{A} > m_{B} v_{B}$
C $m_{A} v_{A} < m_{B} and v_{A} < v_{B}$
D $m_{A} = m_{B} and v_{a} = v_{B}$
Two points masses of 2 kg and 3 kg lie at 5 m and 9 m away from origin O respectively. Find out the distance of centre of mass of these point masses from the origin.
A14.2 m
B7.4 m
C20 m
D6 m