A force of 72 dyne is inclined to the horizontal at an angle of . Find the acceleration in a mass of 9 g, which moves in a horizontal direction.
To solve the problem step by step, we will break it down into manageable parts:
Step 1: Identify the given values
- Force (F) = 72 dyne
- Angle (θ) = 60 degrees
- Mass (m) = 9 g
Step 2: Convert mass to appropriate units
Since we are working with dyne, we need to convert the mass from grams to kilograms for standard SI units. However, since we are using CGS (centimeter-gram-second) units, we can keep the mass in grams.
- Mass (m) = 9 g
Step 3: Find the horizontal component of the force
The horizontal component of the force can be calculated using the cosine of the angle:
Fhorizontal=F⋅cos(θ)
Substituting the values:
Fhorizontal=72⋅cos(60∘)
Step 4: Calculate cos(60∘)
The value of cos(60∘) is:
cos(60∘)=12
Step 5: Substitute the cosine value into the force equation
Now, substituting the value of cos(60∘):
Fhorizontal=72⋅12=36 dyne
Step 6: Apply Newton's second law to find acceleration
According to Newton's second law:
F=m⋅a
Where F is the net force acting on the mass, m is the mass, and a is the acceleration. Rearranging the formula to solve for acceleration gives:
a=Fhorizontalm
Substituting the values:
a=36 dyne9 g
Step 7: Calculate the acceleration
Now, performing the division:
a=4 cm/s2
Final Answer
The acceleration of the mass moving in the horizontal direction is:
4 cm/s2
---
- Force (F) = 72 dyne
- Angle (θ) = 60 degrees
- Mass (m) = 9 g
Since we are working with dyne, we need to convert the mass from grams to kilograms for standard SI units. However, since we are using CGS (centimeter-gram-second) units, we can keep the mass in grams.
- Mass (m) = 9 g
The horizontal component of the force can be calculated using the cosine of the angle:
Fhorizontal=F⋅cos(θ)
Substituting the values:
Fhorizontal=72⋅cos(60∘)
The value of cos(60∘) is:
cos(60∘)=12
Now, substituting the value of cos(60∘):
Fhorizontal=72⋅12=36 dyne
According to Newton's second law:
F=m⋅a
Where F is the net force acting on the mass, m is the mass, and a is the acceleration. Rearranging the formula to solve for acceleration gives:
a=Fhorizontalm
Substituting the values:
a=36 dyne9 g
Now, performing the division:
a=4 cm/s2
The acceleration of the mass moving in the horizontal direction is:
4 cm/s2
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Problems17videos
LAWS OF MOTION : FRICTION
- BOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Self Practice95videos
LAWS OF MOTION : FRICTION
- BOOK - SL ARORACHAPTER - Laws of MotionEXERCISE - Exercise627videos
Laws of Motion
- BOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise20videos
Mathematical tools
Similar Questions
A force of 36 dynes is inclined to the horizontal at an angle of 60∘. Find the acceleration in a mass of 18 g that moves in a horizontal direction.
View SolutionA force of 50N is inclined to the vertical at an angle of 30∘ Find the acceleration it produes in a body of mass 2kg which moves in the horizontal direction .
View Solution
Knowledge Check
- Question 1 - Select One
A body is projected from the ground in a direction inclined to the horizon at an angle of 60∘ . The velocity of projection, given that at a height of 96 ft, the direction of motion is inclined at 30∘ with the horizontal is
A40ft/secB60ft/secC80ft/secD96ft/sec - Question 2 - Select One
An inclined plane makes an angle of 60∘ with horizontal. A disc rolling acceleration equal to:
Ag3B34gCg√3Dg2 - Question 3 - Select One
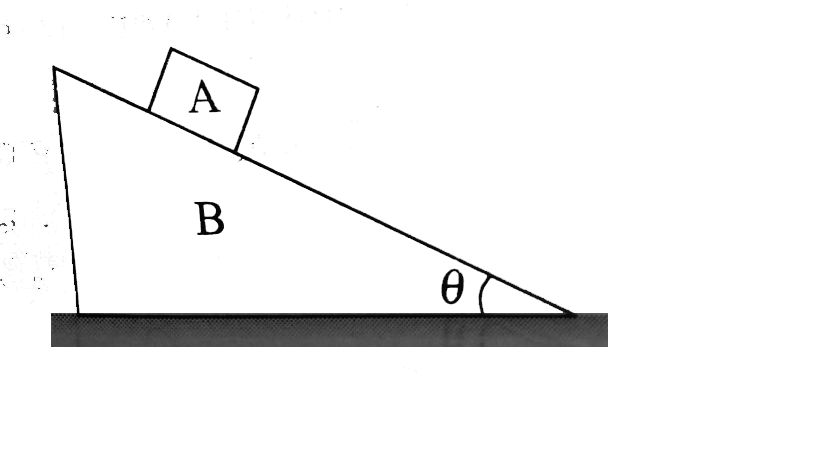
A block is placed on a smooth wedge of inclination angle θ with the horizontal. What minimum acceleration should be given to the wedge in the horizontal direction so that the block starts moving up along the incline?A>gcotθB>>anθC>gsinθD>gcosθ
A force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.
 View Solution
View SolutionA gun (mass =M) fires a bullet (mass =m) with speed vr relative to barrel of the gun which is inclined at an angle of 60∘ with horizontal. The gun is placed over a smooth horizontal surface. Find the recoil speed of gun.
 View Solution
View SolutionA force is inclined at 30o to the horizontal.If its rectangular component in the horizontal direction is 50N ,find the magnitude of the force and its vertical component
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solution

