Fig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
To solve the given problem, we will analyze the position-time graph of the particle and determine the force acting on it during specified time intervals, as well as the impulse at specific times.
Step 1: Analyze the Position-Time Graph for t < 0
- For t<0, the position x is constant.
- Since the position is constant, the velocity v is 0.
- Therefore, the acceleration a is also 0.
- Using Newton's second law, F=m⋅a, where m=4kg:
F=4kg⋅0=0N
Step 2: Analyze the Position-Time Graph for 0 < t < 4 s
- For 0<t<4s, the position x is increasing linearly.
- This indicates that the velocity v is constant.
- The slope of the position-time graph gives the velocity. If the slope is 34, then:
v=34m/s
- Since the velocity is constant, the acceleration a is 0.
- Thus, the force is:
F=4kg⋅0=0N
Step 3: Analyze the Position-Time Graph for t > 4 s
- For t>4s, the position x is again constant.
- This means the velocity v is 0.
- Therefore, the acceleration a is 0.
- Using Newton's second law:
F=4kg⋅0=0N
Step 4: Calculate the Impulse at t = 0 s
- Impulse is defined as the change in momentum:
Impulse=m⋅(vf−vi)
- At t=0:
- Initial velocity vi=0m/s (for t<0)
- Final velocity vf=34m/s (for 0<t<4)
- Therefore:
Impulse=4kg⋅(34−0)=4kg⋅34=3Ns
Step 5: Calculate the Impulse at t = 4 s
- At t=4:
- Initial velocity vi=34m/s (for 0<t<4)
- Final velocity vf=0m/s (for t>4)
- Therefore:
Impulse=4kg⋅(0−34)=4kg⋅(−34)=−3Ns
Final Answers:
1. The force acting on the particle for:
- t<0: 0N
- 0<t<4s: 0N
- t>4s: 0N
2. The impulse at:
- t=0s: 3Ns
- t=4s: −3Ns
- For t<0, the position x is constant.
- Since the position is constant, the velocity v is 0.
- Therefore, the acceleration a is also 0.
- Using Newton's second law, F=m⋅a, where m=4kg:
F=4kg⋅0=0N
- For 0<t<4s, the position x is increasing linearly.
- This indicates that the velocity v is constant.
- The slope of the position-time graph gives the velocity. If the slope is 34, then:
v=34m/s
- Since the velocity is constant, the acceleration a is 0.
- Thus, the force is:
F=4kg⋅0=0N
- For t>4s, the position x is again constant.
- This means the velocity v is 0.
- Therefore, the acceleration a is 0.
- Using Newton's second law:
F=4kg⋅0=0N
- Impulse is defined as the change in momentum:
Impulse=m⋅(vf−vi)
- At t=0:
- Initial velocity vi=0m/s (for t<0)
- Final velocity vf=34m/s (for 0<t<4)
- Therefore:
Impulse=4kg⋅(34−0)=4kg⋅34=3Ns
- At t=4:
- Initial velocity vi=34m/s (for 0<t<4)
- Final velocity vf=0m/s (for t>4)
- Therefore:
Impulse=4kg⋅(0−34)=4kg⋅(−34)=−3Ns
1. The force acting on the particle for:
- t<0: 0N
- 0<t<4s: 0N
- t>4s: 0N
- t=0s: 3Ns
- t=4s: −3Ns
Topper's Solved these Questions
- LAWS OF MOTION : FRICTIONBOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Problems
17 Videos
- LAWS OF MOTION : FRICTIONBOOK - SL ARORACHAPTER - LAWS OF MOTION : FRICTIONEXERCISE - Self Practice
95 Videos
- Laws of MotionBOOK - SL ARORACHAPTER - Laws of MotionEXERCISE - Exercise
627 Videos
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
Similar Questions
Shown the position time graph of a particle of mass 4 kg What is the force on the particle for t<0,0<t<4s motion only
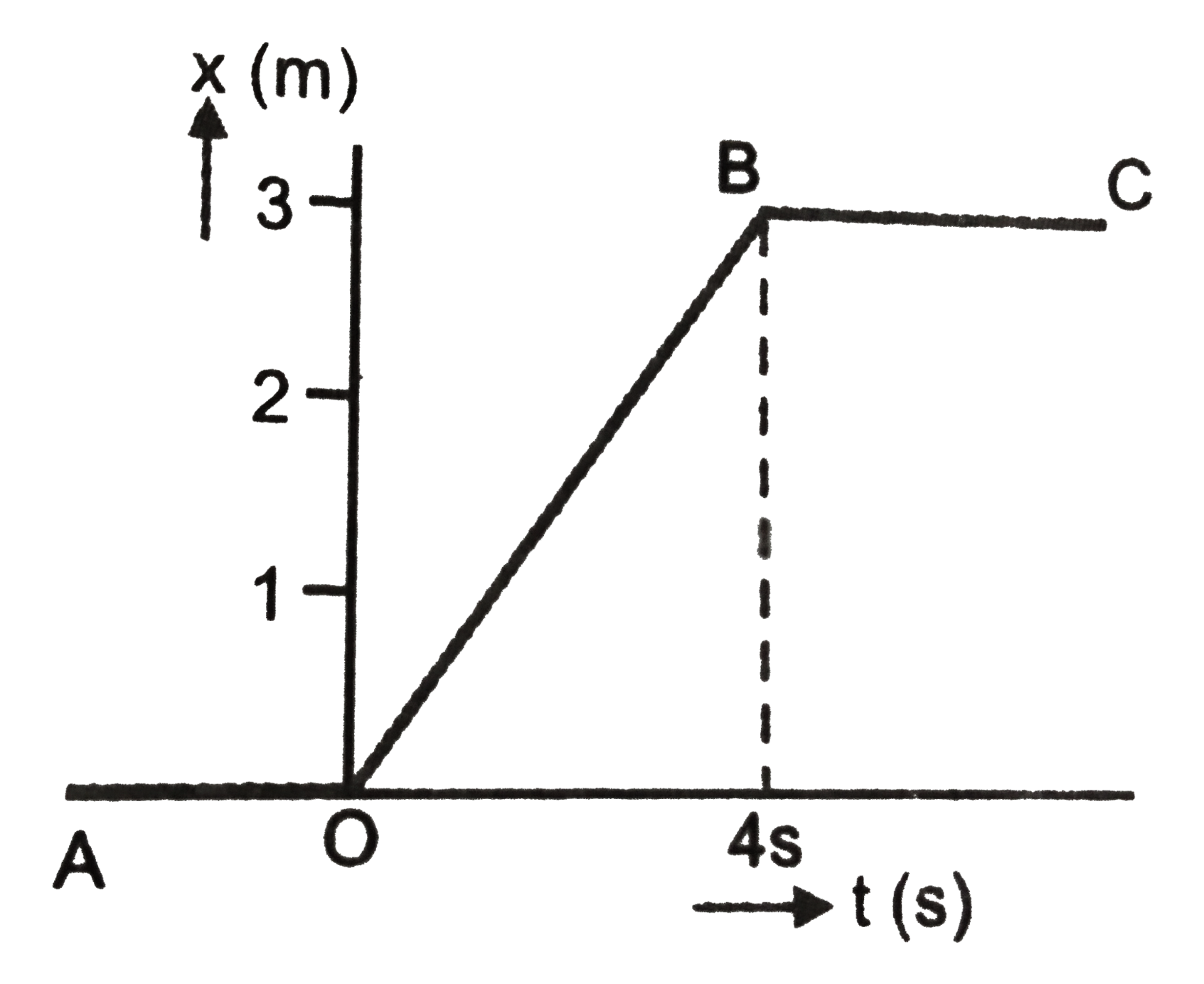 .
.
View SolutionFig. shows the position-time graph of a particle of mass 4 kg. What is the (i) force acting on the particle for t<0,t<4s,0<t<4s? (ii) impulse at t = 0 and t = 4 s? Assume that the motion is one dimensional.
View Solution
Knowledge Check
Figure shows the position time graph of a particle of mass 5kg. The force acting on the particle for 0<t<4s and 8s<t<12s respectively are,
 A5N,5NB5N.7.5NC5N,10ND0N,0N
A5N,5NB5N.7.5NC5N,10ND0N,0NPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is
 A8 JB4 JC0 JDCan't be determined
A8 JB4 JC0 JDCan't be determinedFigure shows the position-time graph of a particle of mass 4kg. Let the force on the particle for t<0 , 0<tlt,4s , t>4s be F1,F2 and F3 respectively. Then
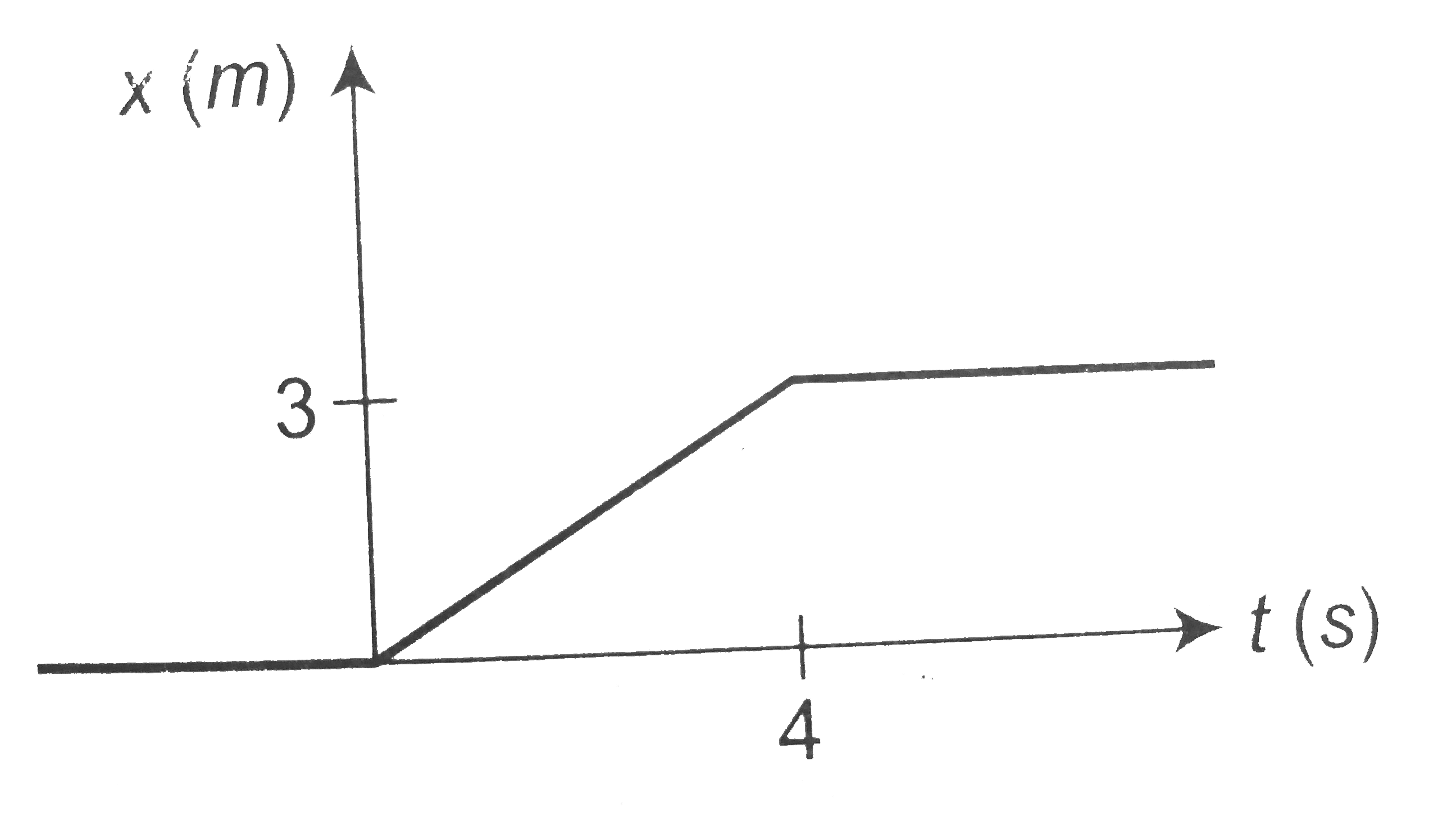 AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
AF1=F2=F3=0BF1>F2=F3CF1>F2>F3DF1<F2<F3
The position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2s is :

View SolutionShows position time graph of a particle of mass 100g Find the impulse at t=0 and at t=4s
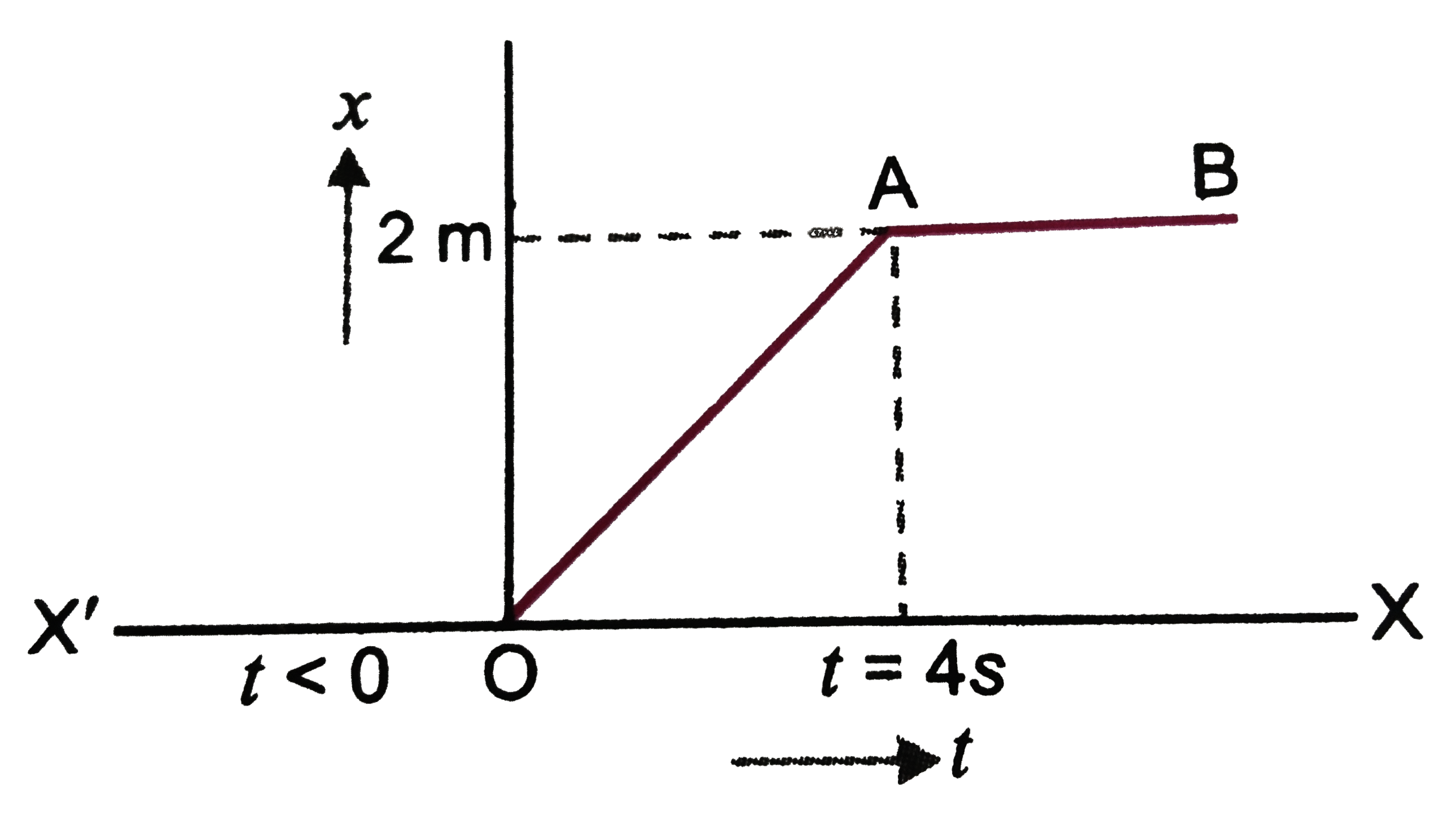 .
.
View SolutionThe position time graph of a body of mass 2kg is as given in What is the impulse on the body at t=0 s and t=4s ?
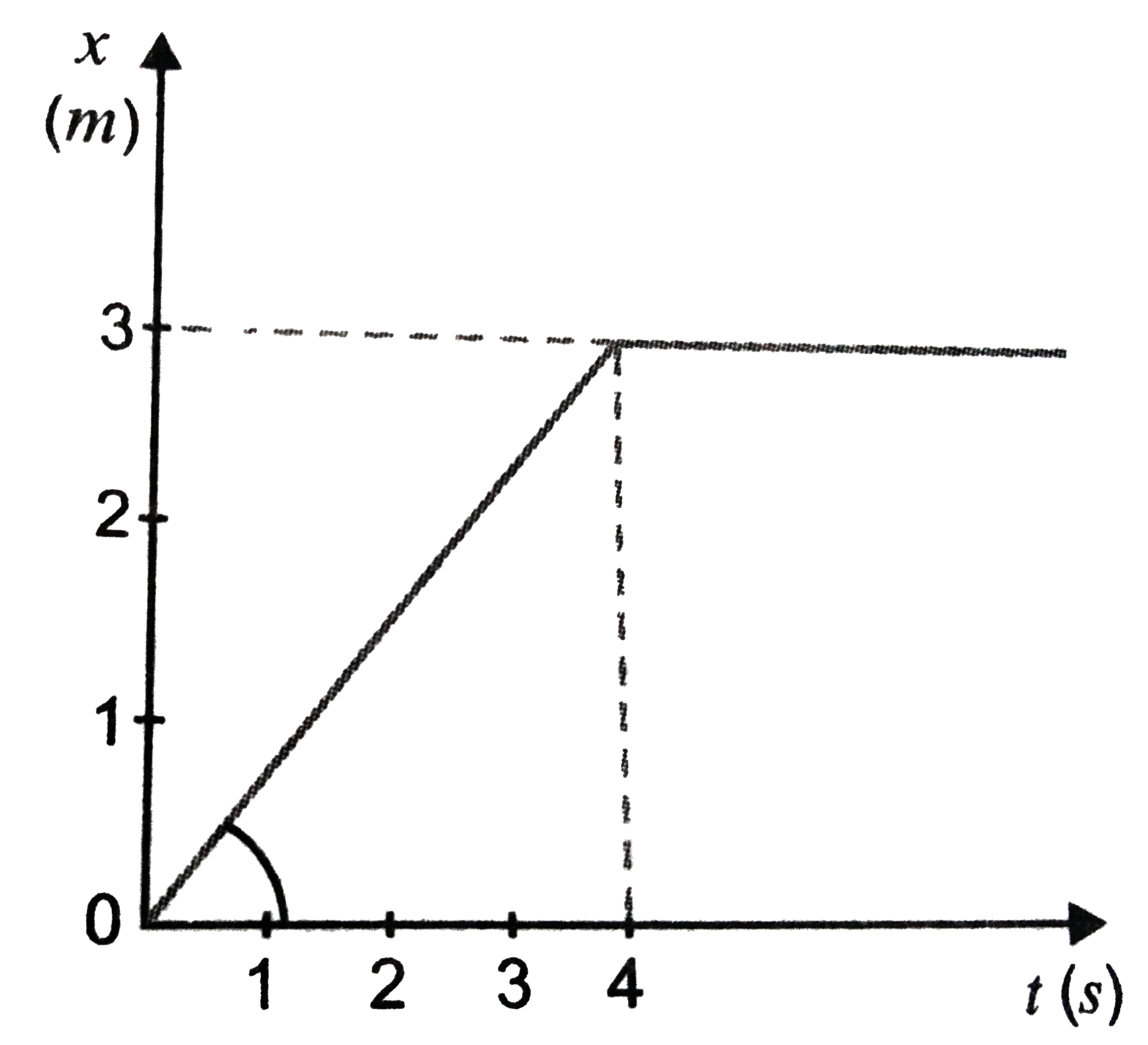 .
.
View SolutionThe position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2s is :

View SolutionIn the figure given, the position-time graph of a particle of mass 0.1 kg is shown the impulse at t = 2s is
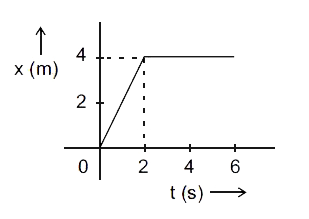
View Solution
