Find the distance travelled by a body before coming rest, if it is moving with a speed of 10ms−1 and the coefficient of friction between the ground and the body is 0.4.
The correct Answer is:12.75m
To find the distance traveled by a body before coming to rest, we can follow these steps:
Step 1: Identify the given values
- Initial speed of the body, u=10m/s
- Final speed of the body, v=0m/s (since it comes to rest)
- Coefficient of friction, μ=0.4
Step 2: Calculate the acceleration due to friction
The force of kinetic friction Fk can be expressed as:
Fk=μ⋅N
where N is the normal force. For a body resting on a horizontal surface, N=mg, where m is the mass of the body and g is the acceleration due to gravity (approximately 9.8m/s2).
Thus, we have:
Fk=μ⋅mg=0.4⋅mg
The acceleration (or retardation, since it is acting opposite to the direction of motion) a can be calculated using Newton's second law:
F=ma
So,
a=Fkm=0.4⋅mgm=0.4g
Since this is a retardation, we take it as negative:
a=−0.4g
Step 3: Substitute the value of g
Using g≈10m/s2:
a=−0.4⋅10=−4m/s2
Step 4: Use the equation of motion to find the distance
We can use the equation of motion:
v2=u2+2aS
where S is the distance traveled.
Substituting the known values:
0=(10)2+2(−4)S
0=100−8S
Step 5: Solve for S
Rearranging the equation gives:
8S=100
S=1008=12.5m
Final Answer
The distance traveled by the body before coming to rest is:
S=12.5m
---
- Initial speed of the body, u=10m/s
- Final speed of the body, v=0m/s (since it comes to rest)
- Coefficient of friction, μ=0.4
The force of kinetic friction Fk can be expressed as:
Fk=μ⋅N
where N is the normal force. For a body resting on a horizontal surface, N=mg, where m is the mass of the body and g is the acceleration due to gravity (approximately 9.8m/s2).
Fk=μ⋅mg=0.4⋅mg
F=ma
So,
a=Fkm=0.4⋅mgm=0.4g
a=−0.4g
Using g≈10m/s2:
a=−0.4⋅10=−4m/s2
We can use the equation of motion:
v2=u2+2aS
where S is the distance traveled.
0=(10)2+2(−4)S
0=100−8S
Rearranging the equation gives:
8S=100
S=1008=12.5m
The distance traveled by the body before coming to rest is:
S=12.5m
Topper's Solved these Questions
Similar Questions
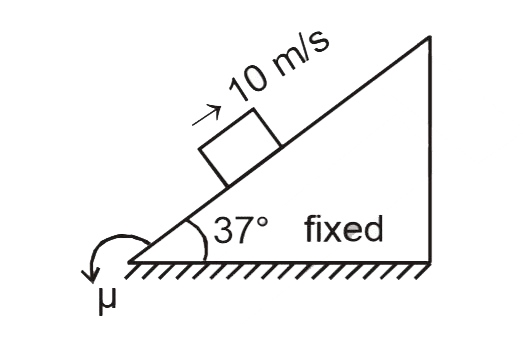
Find out the distance travelled by the block on incline before it stops. Initial velocity of the block is 10 m/s and coefficient of friction between the block and incline is μ=0.5.
View SolutionA body moving on the ground with a velocity of 15m/s comes to rest after covering a distance of 25m If acceleration due to gravity is 10m/s2 Calculate the coefficient of friction between the ground and the body .
View Solution
Knowledge Check
The distance travelled by the moving body is :
AThe area between the speed time graph and time axis.BThe area between the speed time graph and speed axisCThe area between the distance time graph and time axisDThe area between the distance time graph and distance axisA person of mass 72kg sitting on ice pushes a block of mass of 30kg on ice horizontally with a speed of 12ms−1.The coefficient of friction between the man and ice and between block and ice is 0.02.If g=10ms−1,the distance between man and the block, when they come to rest is
A360mB10mC350mD422.5mA man of mass 60kg sitting on ice pushes a block of mass of 12kg on ice horizontally with a speed of 5ms−1.The coefficient of friction between the man and ice and between block and ice is 0.2. If g=10ms−2, the distance between man and the block, when they come to rest is
A6mB6.5mC3mD7m
Find out the distance travelled by the block as shown in figure. If the initial speed of the block is v and μ is the friction coefficient between the surface of block and ground.
View SolutionA body slides down on an inclined plane of inclination 37∘ with horizontal. The distance travelled by the body in time t is given by s=t2. Find the friction coefficient between the body and the incline.
View SolutionA 250 g block slides on aeroug horizontal table. Find the work donen by the frictinal force in bringing the block to rest if it is initially moving at a speed of 40 cm/s. If the friction coefficient between te table and the block is 0.1 how far does the block move before coming to rest?
View SolutionA man of mass 60kg sitting on ice pushes a block of mass 12kg on ice horizontally with a speed of 5ms−1 The coefficient of friction between the man and ice and between block and ice is 0.2Ifg=10ms2 the distance beteen man and the block when they come to rest is .
View SolutionThe brakes of a car moving at 20 m/s along a horizontal road are suddenly applied and it comes to rest after travelling some distance if the coefficient of friction between the tyres and the road is 0.90 and it is assumed that all four tyres behave identically, the shortest distance the car would travel before coming to a stop is
View Solution
