A sphere of radius 0.1m and mass 8π kg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3m. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
Step by step video & image solution for A sphere of radius 0.1m and mass 8 pi kg is attached to the lower end of a steel wire of length 5.0 m and diameter 10^(-3)m. The wire is suspended from 5.22 m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994xx10^(11) N//m^(2)). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
A sphere of radius 0.1m and mass 8πkg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
View SolutionA sphere of radius 10cm and mass 25 kg is attached to the lower end of a steel wire of length 5m and diameter 4mm which is suspended from the ceiling of a room . The point of support is 521cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Ysteel=2×1011N/m2).
View Solution
Knowledge Check
- Question 1 - Select One
A sphere of radius 0.1m and mass 8π kg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3m. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
A7.7ms−1B4.4ms−1C2.2ms−1D8.8ms−1 - Question 2 - Select One
A sphere of mass m attached with the free end of a steel wire of length l swings in the veritical plane form the horizontal positon.
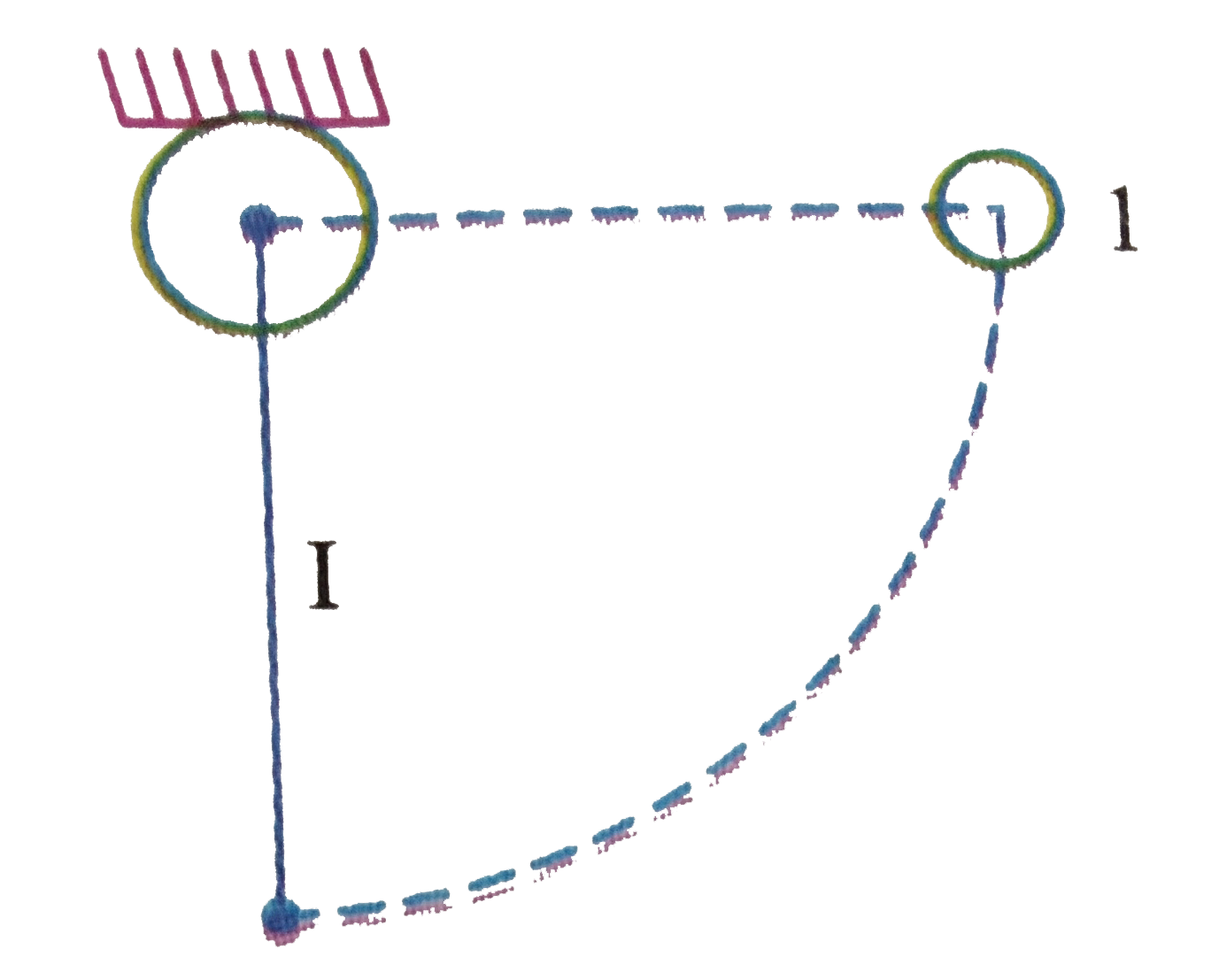
Elongation of the wire in the vericle positon isAmglY(πr2)B2mglY(πr2)Cmgl3Y(πr2)D3mglY(πr2) - Question 3 - Select One
A uniform steel wire of length 3.14 m and diameter 2×10−3 m is fixed at its upper end. When a mass of 10 kg is attached to its lower end, the extension of the wire is 1×10−3 m. The Young's modulus of elasticity is,
A9.8×108N/m2B9.8×109N/m2C9.8×1010N/m2D9.8×1011N/m2
A sphere of radius 10cm and mass 25kg is attached to the lower end of a steel wire which is suspended from the ceiling of a room. The point of support is 521cm above the floor. When the sphere is set swimming as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position.
View SolutionA sphere of radius 1.4 m weighs 500 kg. The sphere
View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View SolutionA sphere of radius 3 cm is drawn into a wire of thickness of 0.5 cm. What is the length of the wire?
View SolutionA sphere of mass m attached with the free end of a steel wire of length l swings in the veritcle plane form the horizontal positon.
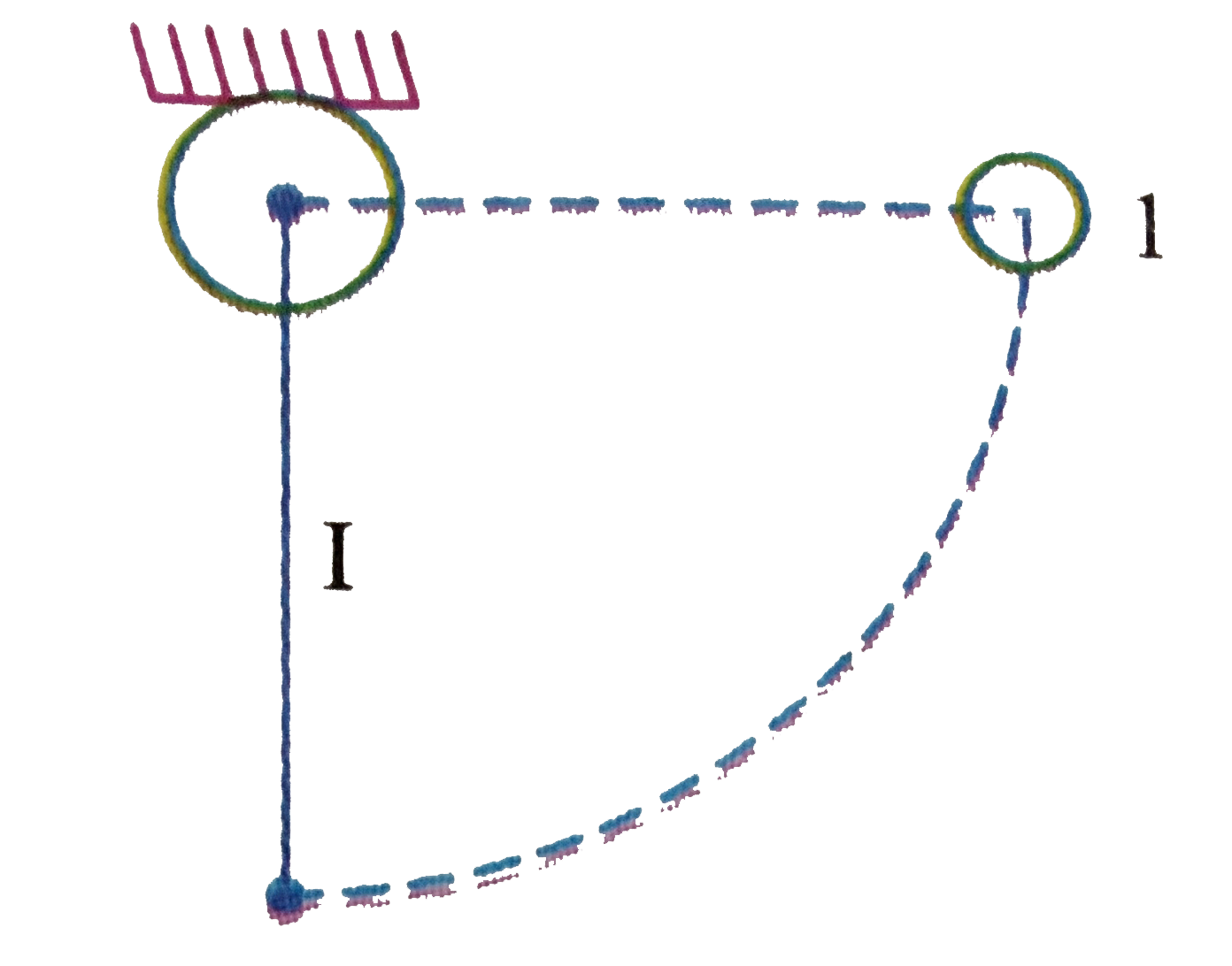
Elastic energy should in the wire in the vericle positon isView Solution

