A tolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is
(a) the period of ensuing oscillation?
(b) the maximum speed of trolley?
(c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces?

Step by step video & image solution for A tolley of mass 3.0kg is connected to two identical spring each of force constant 600Nm^(-1) as shown in figure. If the trolley is displaced from its equilibrium position by 5.0 cm and released, what is (a) the period of ensuing oscillation? (b) the maximum speed of trolley? (c) How much is the total energy dissipated as heat by the time the trolley comes to rest due to damping forces? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Type C Based on Oscillations of a Simple Pendulum7videos
OSCILLATIONS
- BOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Type D Based on Other Examples of SHM2videos
OSCILLATIONS
- BOOK - SL ARORACHAPTER - OSCILLATIONSEXERCISE - Exercise233videos
OSCILLATIONS
- BOOK - SL ARORACHAPTER - MOTION IN ONE DIMENSIONEXERCISE - problems for self practice66videos
MOTION IN ONE DIMENSION
- BOOK - SL ARORACHAPTER - Physical worldEXERCISE - Exercise49videos
Physical world
Similar Questions
A trolley of mass 3.0 kg is connected to two identical rubber bands each of force constant 600Nm−1 as shown in figure. If the trolley is displaced from an equilibrium position by 5.0 cm and released, what is the period of ensuing oscillations?
 View Solution
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
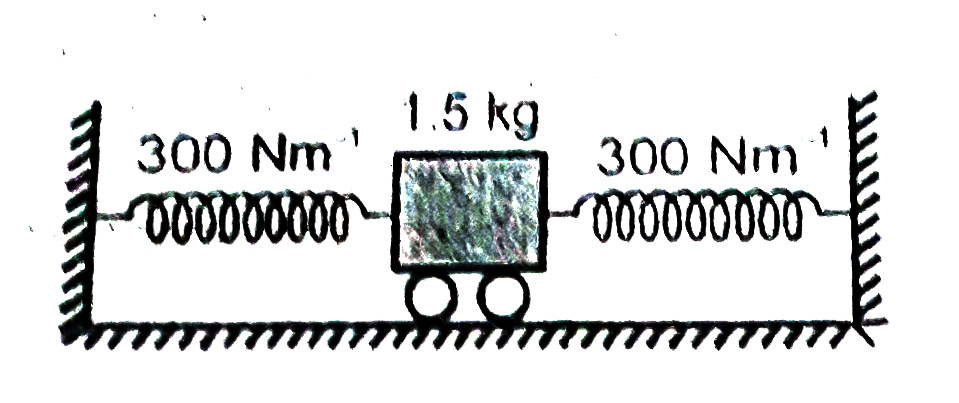 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A trolley of mass M is connected to two springs of force constant K1 and K2 as shown in the figure When the trolley is displacement from its equilibrium postion by a distance a and released , it executes S.H.M of frequency f. If it comes to rest after somtimes due to friction, the total energy dissipated as heat is (Dampling forces are weak)
 Aπ2ma2f2B2π2ma2f2C2a2(K1+K2)D12a2(K1+K2)
Aπ2ma2f2B2π2ma2f2C2a2(K1+K2)D12a2(K1+K2) - Question 2 - Select One
A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
 View Solution
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionTwo blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
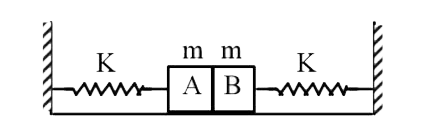 View Solution
View SolutionA cart of mass 2.00kg is attached to the end of a horizontal spring with force constant k=150N/m. The cart is displaced 15.0cm from its equilibrium position and released. What are
(a) the amplitude (b) the period ( c) the mechanical energy (e) the maximum velocity of the cart ? Neglect friction.View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.
 View Solution
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution

