A uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is μ then

f=μ
f=1/(1+μ)
f=1/(1+1/μ)
f=1/(μ+1/μ)
The correct Answer is:C
Step by step video, text & image solution for A uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is mu then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
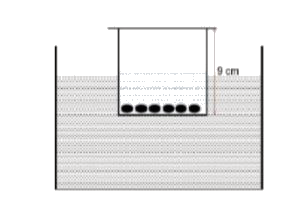
A wide bottom cylindrical massless plastic container of height 9 cm has 40 identical coins inside it and is floating on water with 3 cm inside the water. If we start putting more of such coins on its lid. It is observed that after N coins are put, its equilibrium changes from stable to unstable. Equilibrium in floating is stable if the geometric center of the submerged portion is above the center of mass of the object) The value of N is closed to
View SolutionIf the coefficient of static friction between a table and a uniform massive rope is μ, what fraction of the rope can hang over the edge of a table without the rope sliding.
View SolutionA homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?
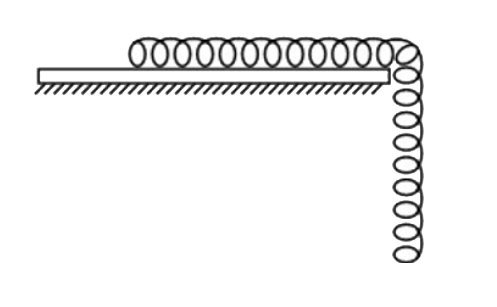
View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
View SolutionA uniform chain of length L hangs partially from table and held in equilibrium by friction. If greatest length of chain that hangs without slipping is l then the coefficient of friction between chain and table is
View SolutionA uniform chain of length L is lying on the horizontal table.If the coefficient of friction between the chain and table top is m, what is the maximum length of the chain that can hang over the edge of the table without disturbing the rest of the chain on the table?
View SolutionL लम्बाई की एक समान रस्सी मेज पर रखी है। यदि घर्षण गुणांक μ है तो रस्सी की अधिकतम लम्बाई जो बिना नीचे फिसले मेज के एक किनारे से लटक सकती है
View SolutionPart of a uniform chain of length L is hanging out of a table. If the coefficient of friction between the chain and the table is , mu estimate the maximum length of the chain that can hang without slipping.
View SolutionA uniform chain of length l is lying on a rough table and 1n th of its length is hanging from the table's edge. If the chain is about to slide off the table the coefficient of friction between the chain and the table is
View SolutionA uniform rope of length L lies on a table. If the coefficient of friction is mu , the maximum fractional length of the hanging part of the rope from the edge of the table without sliding down is
View SolutionA partially hanging L length chain rests on a carved horizontal table. In equilibrium, l can only hang tall. The coefficient of friction between the table and the chain is
View SolutionA uniform rope of length L lies on a table. If the coefficient of friction is μ, the maximum fractional length of the hanging part of the rope from the edge of the table without sliding down is
View SolutionA uniform rope of length L lies on a table. If the coefficient of friction is mu , the maximum fractional length of the hanging part of the rope from the edge of the table without sliding down is
View SolutionA homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is mu . The maximum length which can hang over the table in equilibrium is
View Solution
