$A B C$ is a triangle in vertical plane. Its two base angles $∠ B A C$ and $∠ B C A$ are $45^{\circ}$ and ${tan}^{- 1} \frac{1}{3}$ respectively. A particle is projected from point $A$ such that is passes through vertices $B$ and $C$ . Angle of projectio is $θ$ . Find the value of $3 tan θ$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

Answer

Step by step video, text & image solution for ABC is a triangle in vertical plane. Its two base angles /_BAC and /_BCA are 45^(@) and "tan"^(-1)1/3 respectively. A particle is projected from point A such that is passes through vertices B and C. Angle of projectio is theta. Find the value of 3 tan theta. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS MOTION IN A STRAIGHT LINE

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
$A B C$ is a triangle in vertical plane. Its two base angles $∠ B A C$ and $∠ B C A$ are $45^{\circ}$ and ${tan}^{- 1} (1 / 3)$ respectively. A particle is projected from point A such that it passes through vertices $B$ and $C$ . Find angle of projection in degrees:

A $60^{\circ}$
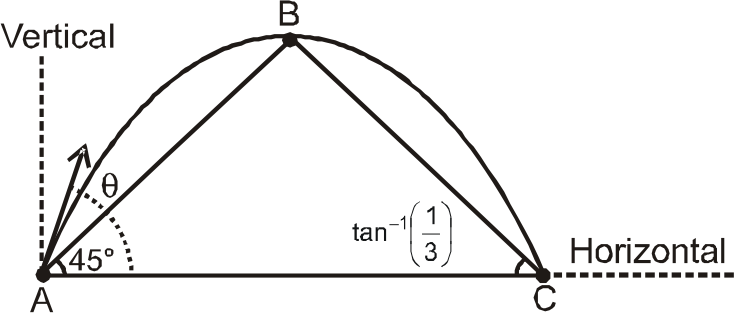B $53^{\circ}$
C ${tan}^{- 1} (5 / 4)$
D ${tan}^{- 1} (5 / 3)$
Question 2 - Select One
In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
A $\frac{a^{2}}{b c}$
B $a + b$
C $\frac{b^{2}}{a c}$
D $\frac{c^{2}}{a b}$
Question 3 - Select One
If $\frac{1 + tan θ}{1 - tan θ} = \sqrt{3}$ , then find the value of $θ$ .
A $30^{\circ}$
B $25^{\circ}$
C $15^{\circ}$
D $45^{\circ}$

DC PANDEY-KINEMATICS-INTEGER_TYPE

Home
Ask Doubt
Profile

ABC is a triangle in vertical plane. Its two base angles ∠BAC and ∠BCA are 45∘ and tan−113 respectively. A particle is projected from point A such that is passes through vertices B and C. Angle of projectio is θ. Find the value of 3tanθ.

The correct Answer is:4

Topper's Solved these Questions

Similar Questions

Knowledge Check

ABC is a triangle in vertical plane. Its two base angles ∠BAC and ∠BCA are 45∘ and tan−1(1/3) respectively. A particle is projected from point A such that it passes through vertices B and C. Find angle of projection in degrees:

In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.

If 1+tanθ1−tanθ=√3 , then find the value of θ.

DC PANDEY-KINEMATICS-INTEGER_TYPE

$A B C$ is a triangle in vertical plane. Its two base angles $∠ B A C$ and $∠ B C A$ are $45^{\circ}$ and ${tan}^{- 1} \frac{1}{3}$ respectively. A particle is projected from point $A$ such that is passes through vertices $B$ and $C$ . Angle of projectio is $θ$ . Find the value of $3 tan θ$ .

$A B C$ is a triangle in vertical plane. Its two base angles $∠ B A C$ and $∠ B C A$ are $45^{\circ}$ and ${tan}^{- 1} (1 / 3)$ respectively. A particle is projected from point A such that it passes through vertices $B$ and $C$ . Find angle of projection in degrees:

If $\frac{1 + tan θ}{1 - tan θ} = \sqrt{3}$ , then find the value of $θ$ .