Question

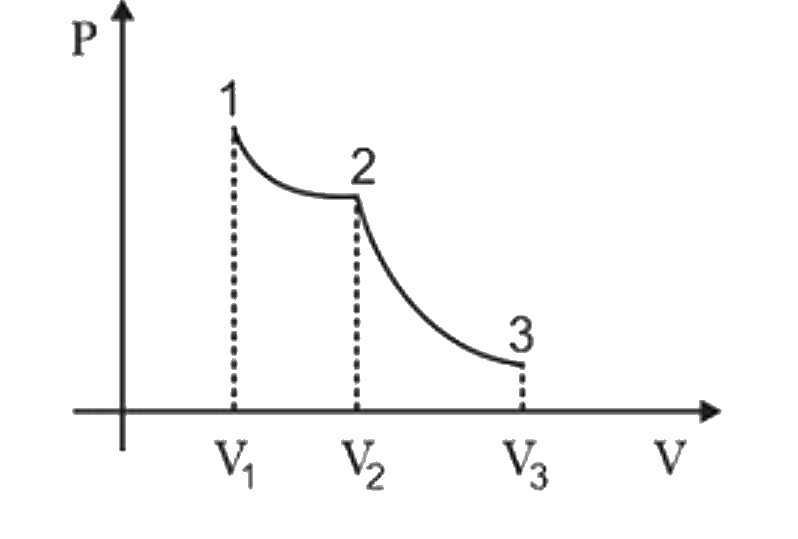
A gass of given mass at a pressure of ${10}^{5}N{m}^{-2}$ expands isothermally until its volume is doubled and then adiabatically until volume is again double. Find the final pressure of the gas. $(\gamma =1.4)$

Answer

`1.89xx10^(4)Nm^(-2)`

Explanation

To solve the problem step by step, we will analyze the two processes the gas undergoes: isothermal expansion and adiabatic expansion.

Step 1: Isothermal Expansion
In the isothermal process, the pressure and volume of the gas are related by the equation:
\( P_1 V_1 = P_2 V_2 \)
where:
- \( P_1 = 10^5 \, \text{N/m}^2 \) (initial pressure)
- \( V_2 = 2V_1 \) (the volume doubles)

Substituting \( V_2 \) into the equation gives:
\( P_1 V_1 = P_2 (2V_1) \)

We can cancel \( V_1 \) from both sides (assuming \( V_1 \neq 0 \)):
\( P_1 = 2P_2 \)

Now, solving for \( P_2 \):
\( P_2 = \frac{P_1}{2} = \frac{10^5}{2} = 5 \times 10^4 \, \text{N/m}^2 \)

Step 2: Adiabatic Expansion
In the adiabatic process, the relationship between pressure and volume is given by:
\( P_2 V_2^\gamma = P_3 V_3^\gamma \)
where:
- \( \gamma = 1.4 \) (given)
- \( V_3 = 2V_2 = 4V_1 \) (the volume doubles again)

Substituting \( V_2 \) and \( V_3 \) into the equation gives:
\( P_2 (2V_1)^\gamma = P_3 (4V_1)^\gamma \)

We can cancel \( V_1^\gamma \) from both sides:
\( P_2 (2^\gamma) = P_3 (4^\gamma) \)

Now, we can express \( 4^\gamma \) as \( (2^2)^\gamma = 2^{2\gamma} \):
\( P_2 (2^\gamma) = P_3 (2^{2\gamma}) \)

Dividing both sides by \( 2^\gamma \):
\( P_3 = \frac{P_2}{2^\gamma} \)

Substituting \( P_2 = 5 \times 10^4 \, \text{N/m}^2 \):
\( P_3 = \frac{5 \times 10^4}{2^{1.4}} \)

Calculating \( 2^{1.4} \):
\( 2^{1.4} \approx 2.639 \)

Now substituting this value:
\( P_3 \approx \frac{5 \times 10^4}{2.639} \approx 1.895 \times 10^4 \, \text{N/m}^2 \)

Final Answer
Thus, the final pressure of the gas after both processes is approximately:
\( P_3 \approx 1.89 \times 10^4 \, \text{N/m}^2 \)

---