A small coil of radius r is placed at the centre of another coaxial coil of radius R(R>>r) find the coeffcient for this pair of coils.
Step by step video & image solution for A small coil of radius r is placed at the centre of another coaxial coil of radius R(Rgtgtr) find the coeffcient for this pair of coils. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A small coil of radius r is placed at the center of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
View SolutionA coil of radius r is placed at the centre of R>>r and coils are in same plane.The coefficient of mutual inductance between the coil is
View Solution
Knowledge Check
- Question 1 - Select One
A small coil of radius r is placed at the centre of a large coil of radius R, where R>>r. The two coils are coplanar. The mutual inductance between the coils is proportional to
Ar/RBr2/RCr2/R2Dr/R2 - Question 2 - Select One
Field at the centre of a circular coil of radius r, through which a current I flows is
ADirectly proportional to rBInversely proportional to ICDirectly proportional to IDDirectly proportional to I2 - Question 3 - Select One
A small, flat coil of resitance r is placed at the centre of a large, closed coil of resistance R. The coils are coplanar. Their mutual inductance is M. Initially a constant current i was flowing in the inner coil. If this curent is suddenly swithced off, what charge will circulate in the outer coil?
AMir/R2BMiR/r2CMi/RDMi/r
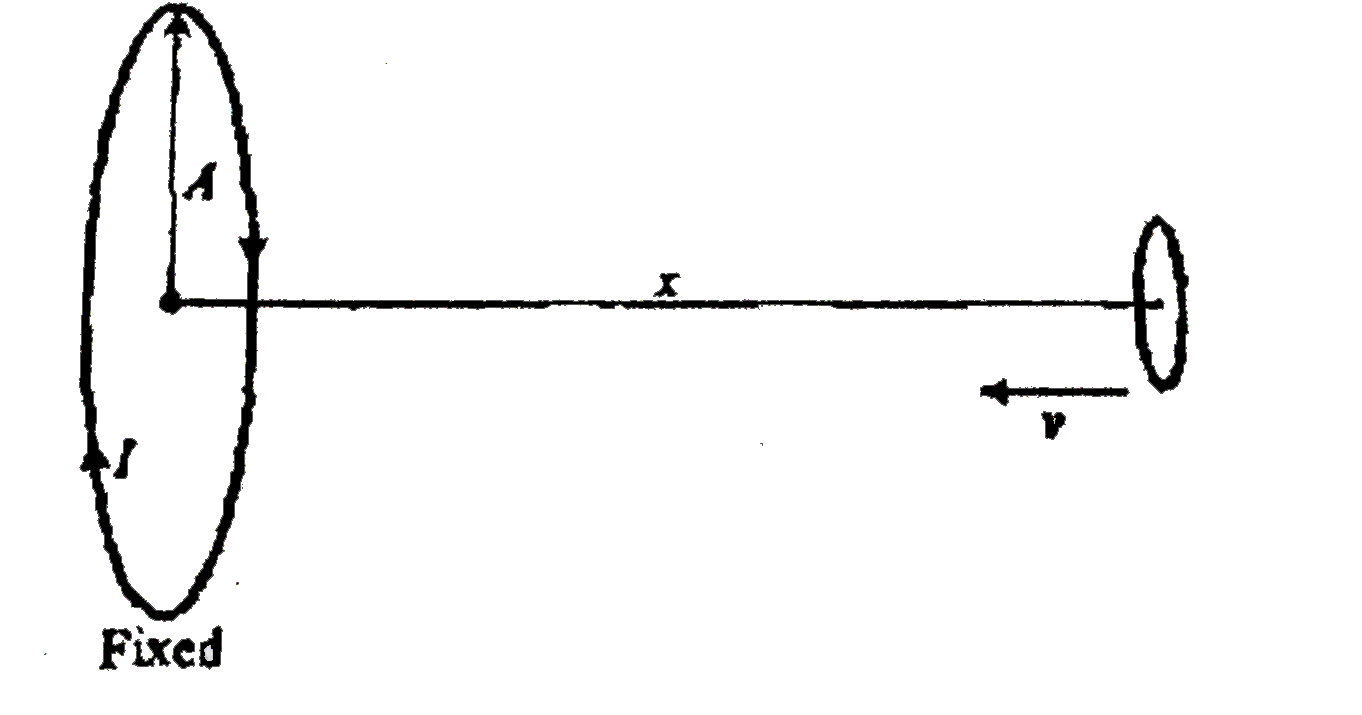
Figure-5.77. shows a fixed coil of N turns and radius a carrying a current I. At a distance x from its centre another small coaxial coil of radius b(b<<a) and resistance R is moving toward the first coil at a uniform speed v. Find the induced current in smaller coil.
 View Solution
View SolutionA flat coil of area A and n turns is placed at the centre of a ring fo radius r(r2>>A) and resistance R. The coil and the ring are coplaner. When the current in the coil increases from zero to i , the total charge circulating in the ring is
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
View SolutionThe magnetic field at the centre of a circular coil of radius r carrying current l is B1. The field at the centre of another coil of radius 2r carrying same current l is B2. The ratio B1B2 is
View SolutionThe magnetic field produced at the center of a current carrying circular coil of radius r, is
View Solution

