Two concentric circular coils of radius and are placed coaxially with centres coinciding If then calculate the mutual inductance the coils.
To calculate the mutual inductance between two concentric circular coils with radii r (small coil) and R (large coil), where R≫r, we can follow these steps:
1. Understanding the Setup:
- We have two coils: a smaller coil with radius r and a larger coil with radius R.
- The coils are coaxially placed, meaning they share the same center.
2. Magnetic Field due to the Larger Coil:
- The magnetic field B at the center of the larger coil (which affects the smaller coil) can be expressed as:
B=μ0I2R
- Here, μ0 is the permeability of free space, and I is the current flowing through the larger coil.
3. Calculating the Area of the Smaller Coil:
- The area A of the smaller coil is given by:
A=πr2
4. Calculating the Magnetic Flux through the Smaller Coil:
- The magnetic flux Φ through the smaller coil due to the magnetic field from the larger coil is given by:
Φ=B⋅A=(μ0I2R)⋅(πr2)
- Substituting the expressions for B and A:
Φ=μ0Iπr22R
5. Finding Mutual Inductance:
- The mutual inductance M between the two coils is defined as the ratio of the magnetic flux through one coil due to the current in the other coil to the current itself:
M=ΦI
- Substituting the expression for Φ:
M=μ0Iπr22RI=μ0πr22R
6. Final Expression for Mutual Inductance:
- Therefore, the mutual inductance M between the two coils is:
M=μ0πr22R
- We have two coils: a smaller coil with radius r and a larger coil with radius R.
- The coils are coaxially placed, meaning they share the same center.
- The magnetic field B at the center of the larger coil (which affects the smaller coil) can be expressed as:
B=μ0I2R
- Here, μ0 is the permeability of free space, and I is the current flowing through the larger coil.
- The area A of the smaller coil is given by:
A=πr2
- The magnetic flux Φ through the smaller coil due to the magnetic field from the larger coil is given by:
Φ=B⋅A=(μ0I2R)⋅(πr2)
- Substituting the expressions for B and A:
Φ=μ0Iπr22R
- The mutual inductance M between the two coils is defined as the ratio of the magnetic flux through one coil due to the current in the other coil to the current itself:
M=ΦI
- Substituting the expression for Φ:
M=μ0Iπr22RI=μ0πr22R
- Therefore, the mutual inductance M between the two coils is:
M=μ0πr22R
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-3 PART 2
Explore 16 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:HLP
Explore 39 Videos
Similar Questions
Two circular loops of radius r and R (R>>r) are placed coaxially with their centres coinciding. What will be the mutual inductance for the pair? If one of the coils is rotated through 90∘ angle, then what will be the new mutual inductance?
View SolutionTwo concentric circular coil,s one of small radius r1 and the other of large radius r2, such that r1<<r2, are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View Solution
Knowledge Check
Two concentric circular coils, one of small radius r1and the other of large radiusr2 such that r1<<r2 are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
Aμ0πtr212r2Bμ0πtr222r1Cμ0πtr22r1Dμ0πtr21r2Two concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
 Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22r
Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22r
Two conducting circular loops of radii R1 and R2 are placed in the same plane with their centres coinciding. If R1 >> R2 the mutual inductance M between them will be directly proportional to
View Solution(a) Explain the meaning of the term mutual inductance. Consider two concentric circular coils, one radius r1 and the other of radius r2(r1<r2) placed coaxially with centres coinciding with each other. Obtain the expression for the mutual inductance of the arrangement.
(b) A rectangular coil of area A, having number of turns N is rotated at 'f' revoluation per second in a uniform magnetic field B, the field being perpendicular to the coil. Prove that maximum emf induced in the coil is 2πfNBA.
View SolutionTwo concentric circular coils, one of small radius r and the other of large radius R, such that R >> T, are placed coaxially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionTwo circular coils, one of smaller radius r1 and the other of very large radius r2 are placed co-axially with centres coinciding. Obtain the mutual inductance of the arrangement.
View SolutionA coil of radius r is placed at the centre of R>>r and coils are in same plane.The coefficient of mutual inductance between the coil is
View SolutionO is the centre of two coplanar concentric circular conductors, A and B, of radii r and R respectively as shown in the figure. Here, r<<<R. The mutual inductance of the system of the conductors can be given by
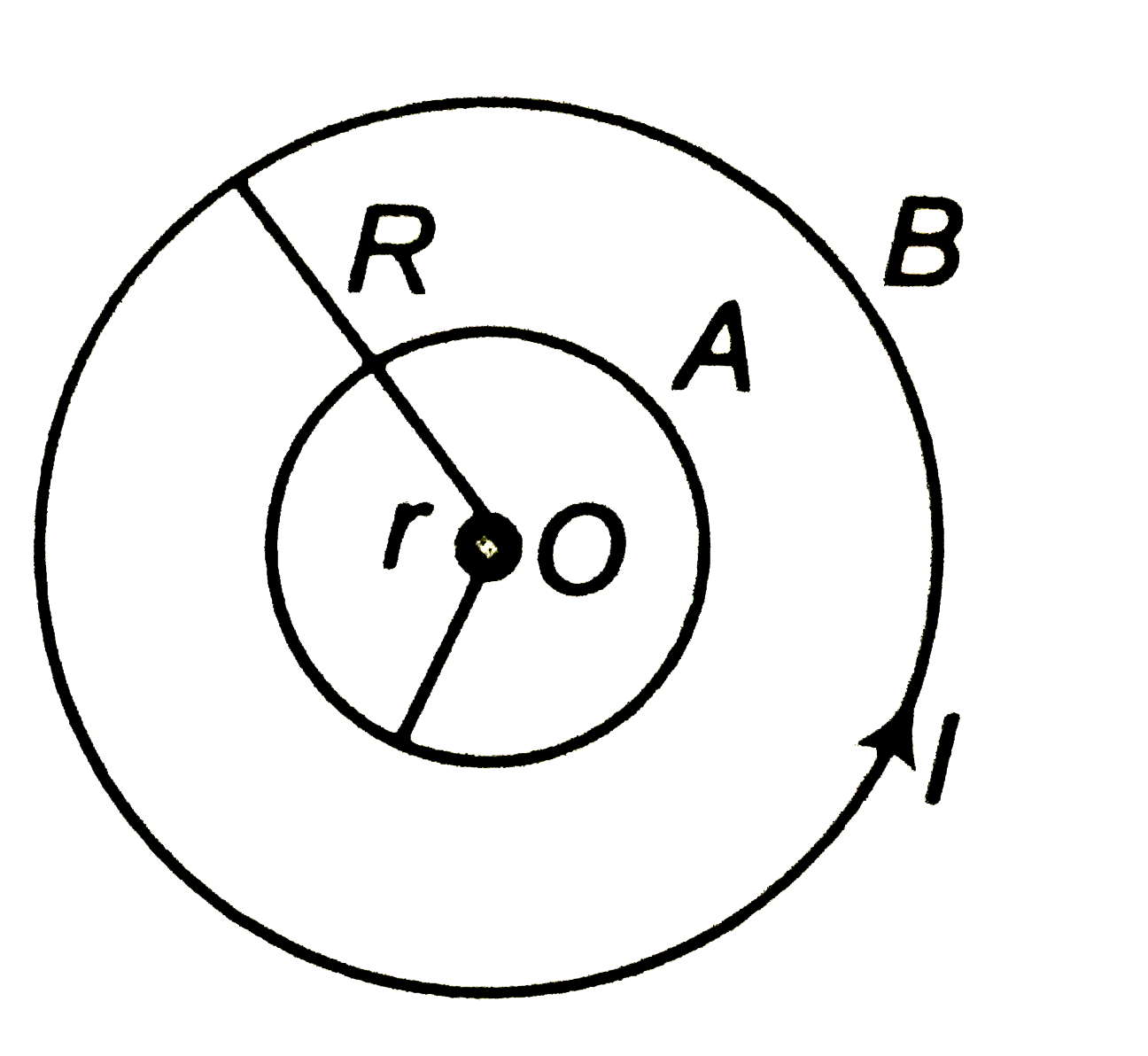
View Solution