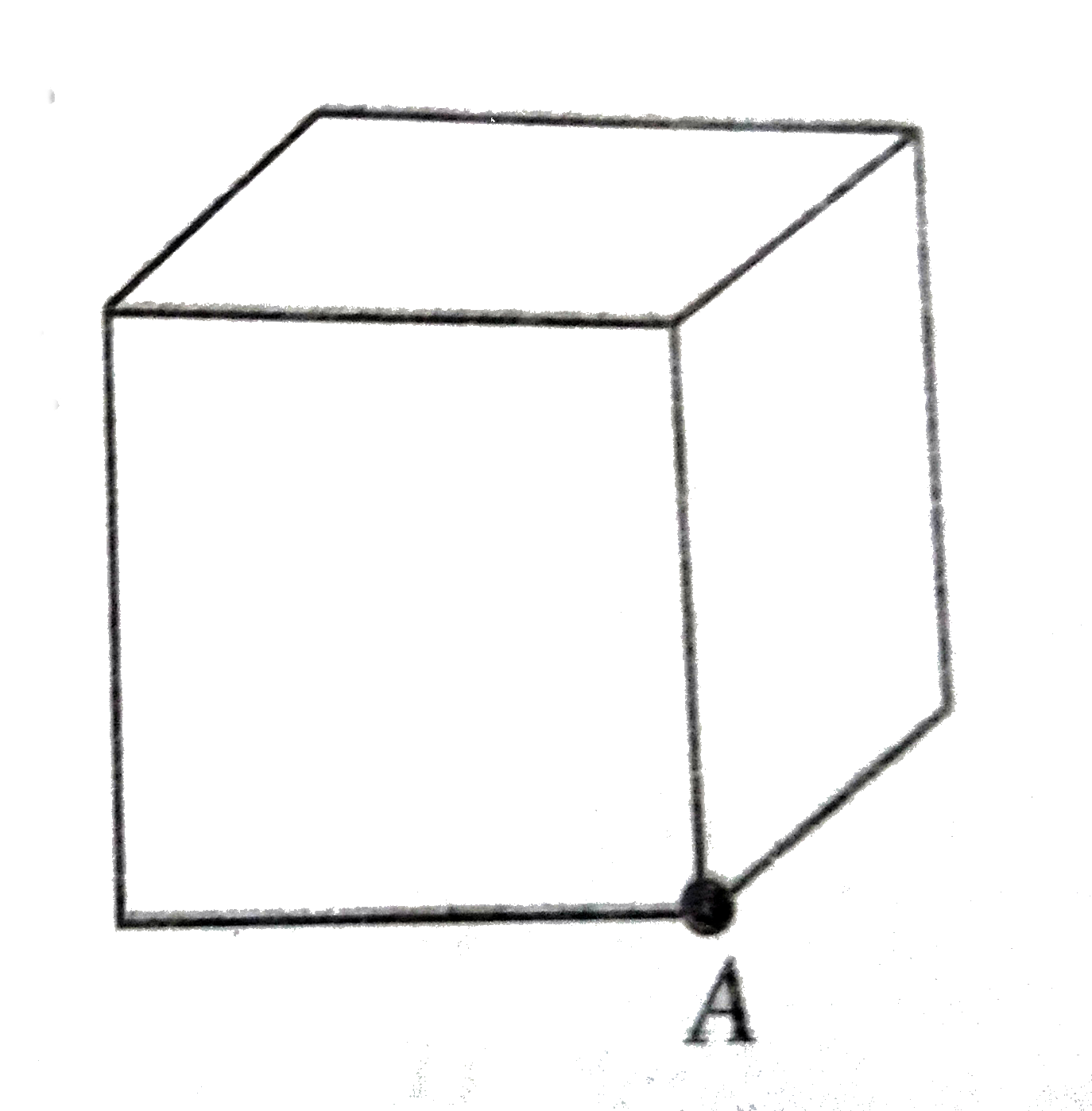
The total electric flux through a cube when a charge 8q is placed at one corner of the cube is
ε0q
ε0q
qε0
q4πε0
The correct Answer is:C
To solve the problem of finding the total electric flux through a cube when a charge of 8Q is placed at one corner of the cube, we can follow these steps:
1. Understand the Configuration:
- We have a cube, and a charge of 8Q is placed at one of its corners.
2. Apply Gauss's Law:
- According to Gauss's Law, the total electric flux (Φ) through a closed surface is given by:
Φ=Qencϵ0
- Here, Qenc is the total charge enclosed by the surface, and ϵ0 is the permittivity of free space.
3. Consider the Symmetry:
- The charge 8Q at the corner of the cube is shared by eight identical cubes that can be imagined to surround the charge. Each of these cubes will have an equal share of the total flux.
4. Calculate the Total Flux for All Cubes:
- The total electric flux through all eight cubes can be calculated as:
Φtotal=8Qϵ0
5. Determine the Flux Through One Cube:
- Since the total flux is equally distributed among the eight cubes, the flux through one cube (Φcube) is:
Φcube=Φtotal8=8Qϵ0⋅8=Qϵ0
6. Final Result:
- Therefore, the total electric flux through the cube when a charge 8Q is placed at one corner is:
Φ=Qϵ0
Conclusion:
The total electric flux through the cube is Qϵ0.
- We have a cube, and a charge of 8Q is placed at one of its corners.
- According to Gauss's Law, the total electric flux (Φ) through a closed surface is given by:
Φ=Qencϵ0
- Here, Qenc is the total charge enclosed by the surface, and ϵ0 is the permittivity of free space.
- The charge 8Q at the corner of the cube is shared by eight identical cubes that can be imagined to surround the charge. Each of these cubes will have an equal share of the total flux.
- The total electric flux through all eight cubes can be calculated as:
Φtotal=8Qϵ0
- Since the total flux is equally distributed among the eight cubes, the flux through one cube (Φcube) is:
Φcube=Φtotal8=8Qϵ0⋅8=Qϵ0
- Therefore, the total electric flux through the cube when a charge 8Q is placed at one corner is:
Φ=Qϵ0
The total electric flux through the cube is Qϵ0.
Topper's Solved these Questions
- ELECTROSTATICSBook:TARGET PUBLICATIONChapter:ELECTROSTATICSExercise:EVALUATION TEST
Explore 14 Videos
- ELECTROSTATICSBook:TARGET PUBLICATIONChapter:ELECTROSTATICSExercise:CRITICAL THINKING
Explore 67 Videos
- ELECTROMAGNETIC INDUCTIONBook:TARGET PUBLICATIONChapter:ELECTROMAGNETIC INDUCTIONExercise:EVALUATION TEST
Explore 8 Videos
- GRAVITATIONBook:TARGET PUBLICATIONChapter:GRAVITATIONExercise:EVALUATION TEST
Explore 24 Videos
Similar Questions
Knowledge Check
The total electric flux through a cube when a charge 8q is placed at one comer of the cube is
Aε0qBε0qC4πε0qDqε0Electric flux through a cube with charge q inside is
Aqε0Bq6ε0Cq3ε0D0A point charge q is kept at a corner of a cube
AElectric flux linked with individual faces of the cube may be zeroBElectric flux linked with individual faces of the cube may be non-zeroCElectric flux linked with a certain face of the cube may be q/8ε0DElectric flux linked with a certain face of the cube may be q/24ε0
Find the flux through shaded region, due to charge Q placed at vertex of a cube
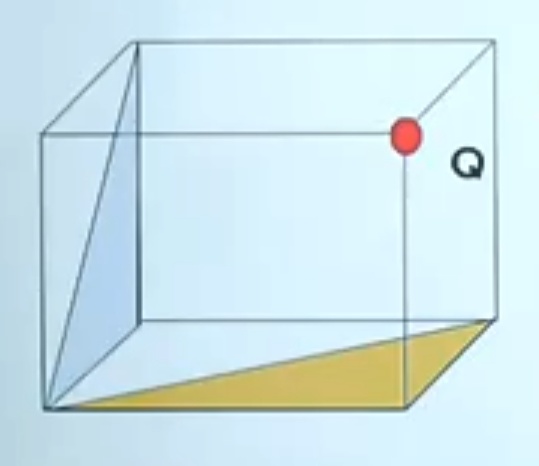
View SolutionTwelve charges have been placed at the centre of each side of a cube as shown in the figure. Find the magnitude of Electric force acting on a charge Q placed at the centre of the cube. Take the side length of the cube to be r.
View SolutionWhat is the flux link through a cube of side l if a charge 2q is placed at one end of cube ?
View SolutionWhat is the electric flux if a charge is placed in one corner of a Cube of length l :
View SolutionIf 8 identical charges of -g each are placed at the eight corners of a cube of side b, then electrostatic potential energy of a charge +q0 placed at the centre of the cube will be
View Solution