15x + 5y =-8
y+4 =-3x
How many solutions does the system above have ?
0
1
2
An infinite number
The correct Answer is:A
To determine how many solutions the system of equations has, we will analyze the given equations step by step.
Given Equations:
1. 15x+5y=−8 (Equation 1)
2. y+4=−3x (Equation 2)
Step 1: Rewrite the second equation in standard form
We can rearrange Equation 2 to express it in the standard form Ax+By+C=0.
Starting with:
y+4=−3x
We can move 3x to the left side:
3x+y+4=0
Step 2: Identify coefficients
Now we have two equations in standard form:
1. 15x+5y+8=0 (from Equation 1)
2. 3x+y+4=0 (from Equation 2)
From these equations, we can identify:
- For Equation 1: A1=15,B1=5,C1=8
- For Equation 2: A2=3,B2=1,C2=4
Step 3: Calculate the ratios of coefficients
Next, we will calculate the ratios of the coefficients A1/A2, B1/B2, and C1/C2:
1. A1A2=153=5
2. B1B2=51=5
3. C1C2=84=2
Step 4: Analyze the ratios
Now we compare the ratios:
- A1A2=5
- B1B2=5
- C1C2=2
We see that:
- A1A2=B1B2 (both equal to 5)
- C1C2 is not equal to A1A2 or B1B2 (it equals 2)
Conclusion
Since A1A2=B1B2 but C1C2 is not equal to these ratios, the system of equations has no solutions. This means the lines represented by these equations are parallel and do not intersect.
Final Answer
The system has 0 solutions.
---
1. 15x+5y=−8 (Equation 1)
2. y+4=−3x (Equation 2)
We can rearrange Equation 2 to express it in the standard form Ax+By+C=0.
y+4=−3x
3x+y+4=0
Now we have two equations in standard form:
1. 15x+5y+8=0 (from Equation 1)
2. 3x+y+4=0 (from Equation 2)
- For Equation 1: A1=15,B1=5,C1=8
- For Equation 2: A2=3,B2=1,C2=4
Next, we will calculate the ratios of the coefficients A1/A2, B1/B2, and C1/C2:
2. B1B2=51=5
3. C1C2=84=2
Now we compare the ratios:
- A1A2=5
- B1B2=5
- C1C2=2
- A1A2=B1B2 (both equal to 5)
- C1C2 is not equal to A1A2 or B1B2 (it equals 2)
Since A1A2=B1B2 but C1C2 is not equal to these ratios, the system of equations has no solutions. This means the lines represented by these equations are parallel and do not intersect.
The system has 0 solutions.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
4x−2y+3=8
3x+6y=8y−x+5
How many solutions does the system of equations shown above have?A0B1C2DIndinitely many - Question 2 - Select One

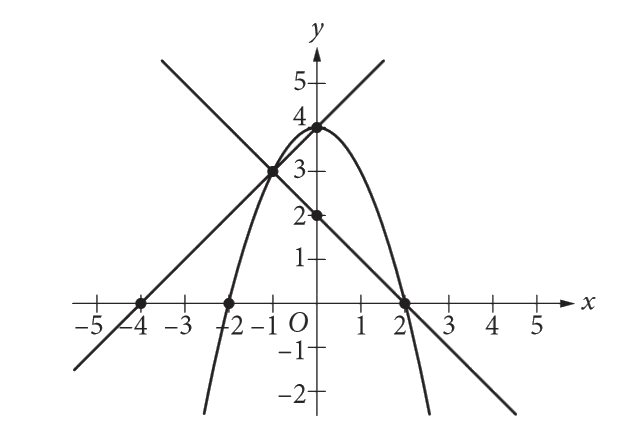
A system of three equations is shown graphically in the xy-plane above. How many solutions does the system have ?A0B2C3D5 - Question 3 - Select One
y=x2+3x−7
y-5x+8=0
How many solutions are there to the system of equations above?AThere are exactly 4 solutionsBThere are exactly 2 solutionsCThere is exactly 1 solution.DThere are no solutions
x2+y2=160
y=3x
If (x,y) is a solutions to the system of equations above, what is the value of y2?View Solution4x+6y=12
y=80−kx
For what value of k does the system of equation above have no solution?View Solution2x-3y=-14
3x-2y=-6
If (x ,y) is a solution to the system of equations above, what is the value of x − y ?View Solutiony=3h−2x+5
hy−8x=5
For what value of h does the system of equations above have no solution?View Solution{(-2x+5y=1), (7x-10y=-11):}
If (x,y) is a solution to the system of equations above, what is the sum of x and y?View Solution