The plate separation in a parallel plate condenser and plate area is A. If it is charged to V volt battery is diconnected then the work done increasing the plate separation to 2d will be
32ε0AV2d
ε0AV2d
2ε0AV2d
ε0AV22d
The correct Answer is:D
To solve the problem of calculating the work done in increasing the plate separation of a parallel plate capacitor from d to 2d after disconnecting the battery, we can follow these steps:
1. Understand the Initial Conditions:
- The capacitor is charged to a voltage V when connected to a battery.
- The initial plate separation is d and the area of the plates is A.
2. Calculate the Initial Charge:
- The capacitance C of a parallel plate capacitor is given by:
C=ϵ0Ad
- The charge Q on the capacitor when charged to voltage V is:
Q=C⋅V=ϵ0AVd
3. Calculate Initial Potential Energy:
- The initial potential energy Ui stored in the capacitor is given by:
Ui=Q22C=Q22(ϵ0Ad)=Q2d2ϵ0A
- Substitute Q=ϵ0AVd:
Ui=(ϵ0AVd)2d2ϵ0A=ϵ0AV22d
4. Calculate Final Capacitance:
- When the plate separation is increased to 2d, the new capacitance Cf is:
Cf=ϵ0A2d
5. Calculate Final Potential Energy:
- The final potential energy Uf is:
Uf=Q22Cf=Q22(ϵ0A2d)=Q2⋅2d2ϵ0A=Q2dϵ0A
- Substitute Q=ϵ0AVd:
Uf=(ϵ0AVd)2dϵ0A=ϵ0AV2d
6. Calculate Work Done:
- The work done W in increasing the plate separation is the change in potential energy:
W=Uf−Ui=ϵ0AV2d−ϵ0AV22d
- Simplifying:
W=ϵ0AV2d(1−12)=ϵ0AV2d⋅12=ϵ0AV22d
Final Answer:
The work done in increasing the plate separation from d to 2d is:
W=ϵ0AV22d
- The capacitor is charged to a voltage V when connected to a battery.
- The initial plate separation is d and the area of the plates is A.
- The capacitance C of a parallel plate capacitor is given by:
C=ϵ0Ad
- The charge Q on the capacitor when charged to voltage V is:
Q=C⋅V=ϵ0AVd
- The initial potential energy Ui stored in the capacitor is given by:
Ui=Q22C=Q22(ϵ0Ad)=Q2d2ϵ0A
- Substitute Q=ϵ0AVd:
Ui=(ϵ0AVd)2d2ϵ0A=ϵ0AV22d
- When the plate separation is increased to 2d, the new capacitance Cf is:
Cf=ϵ0A2d
- The final potential energy Uf is:
Uf=Q22Cf=Q22(ϵ0A2d)=Q2⋅2d2ϵ0A=Q2dϵ0A
- Substitute Q=ϵ0AVd:
Uf=(ϵ0AVd)2dϵ0A=ϵ0AV2d
- The work done W in increasing the plate separation is the change in potential energy:
W=Uf−Ui=ϵ0AV2d−ϵ0AV22d
- Simplifying:
W=ϵ0AV2d(1−12)=ϵ0AV2d⋅12=ϵ0AV22d
The work done in increasing the plate separation from d to 2d is:
W=ϵ0AV22d
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
A parallel plate capacitor is charged and then isolated. On increasing the plate separation
View SolutionA.P.D. of V volts is applied across the plates of a parallel plate capacitor having plate area A. if Q is the charge on its plates and K is the dielectric constant of the medium, between the plates, then the plate separation is given by
View Solution
Knowledge Check
The plate separation in a parallel plate condenser and plate area is A. If it is charged to V volt battery is diconnected then the work done increasing the plate separation to 2d will be
A32ε0AV2dBε0AV2dC2ε0AV2dDε0AV22dA parallel plate capacitor is charged and then isolated. On increasing the plate separation
A Charge Potential Difference Capacitanceremains constant remains constant decreasesB Charge Potential Difference Capacitanceremains constant increases decreasesC Charge Potential Difference Capacitanceremains constant decreases increasesD Charge Potential Difference Capacitanceincreases decreases increasesA parallel plate capacitor of plate are A and plate separation d is charged by a battery of voltage V. The battery is then disconnected. The work needed to pull the plates to a separation 2d is
AAv2ε0dB2Av2ε0dCAv2ε02dD3Av2ε02d
A parallel plate capacitor has area of each plate A, the separation between the plates is d. It is charged to a potential V and then disconnected from the battery. The amount of work done in the filling the capacitor Completely with a dielectric constant k is.
View SolutionThe plates of a parallel plate capacitor are charged by a battery and the battery is disconnected after the charging. Now, the plates are placed as shown in the figure. Then (plates are not parallel to each other).
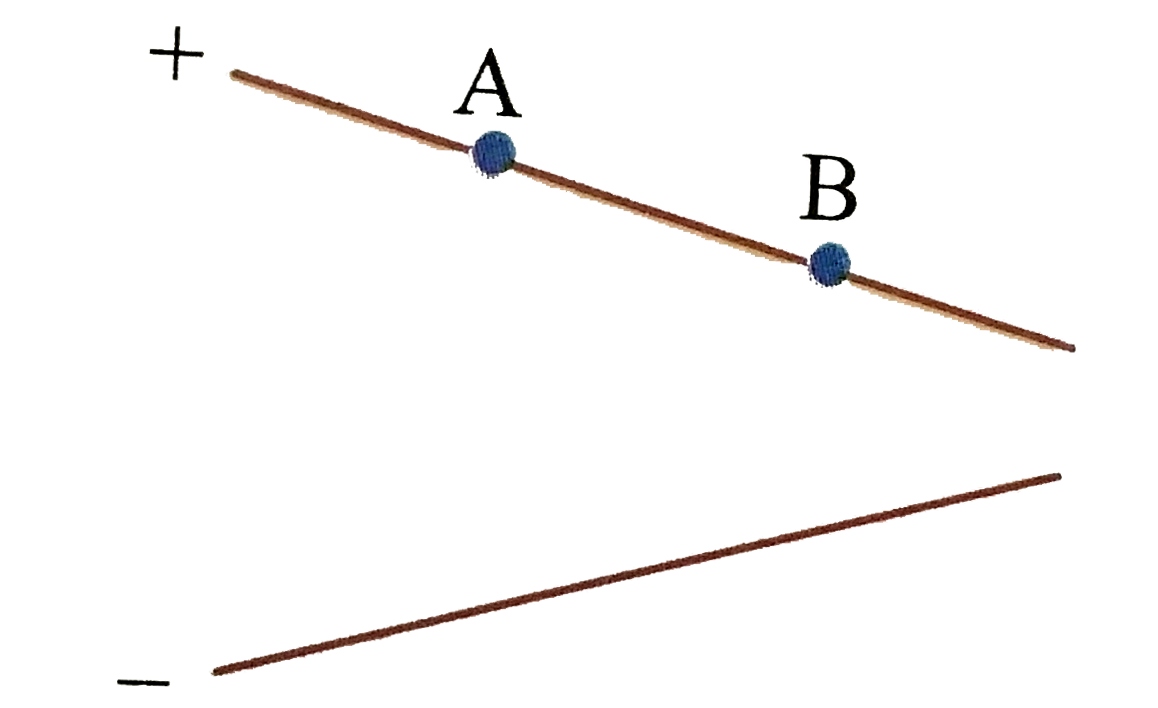 .
.
View SolutionTwo metal plates are separated by a distance d in a parallel plate condenser. A metal plate of thickness t and of the same area is inserted between the condenser plates. The value of capacitance increases by ….times.
View SolutionOn increasing the plate separation of a charged condenser, the energy
View SolutionThe parallel plates of a condenser are separated by an insulating material. It is because of
View Solution
