A solid body X of very large heat capacity is kept in an atmosphere whose temperature is 300 K. The body X is connected to a rod of length 1 m and cross sectional area S, as shown in the figure. Thermal conductivity of rod AB is 0.0567W/mK. Assuming that there is no heat exchange with the surrounding except fom the end B of the rod i.e., neither by any surface of X nor by the curved surface of rod. The end B has emissivity e=0.8. If the steady state temperature of the end B is 400 K then find the temperature of X in steady state. (Stefan constant σ−5.67×10−8W/m2K4)
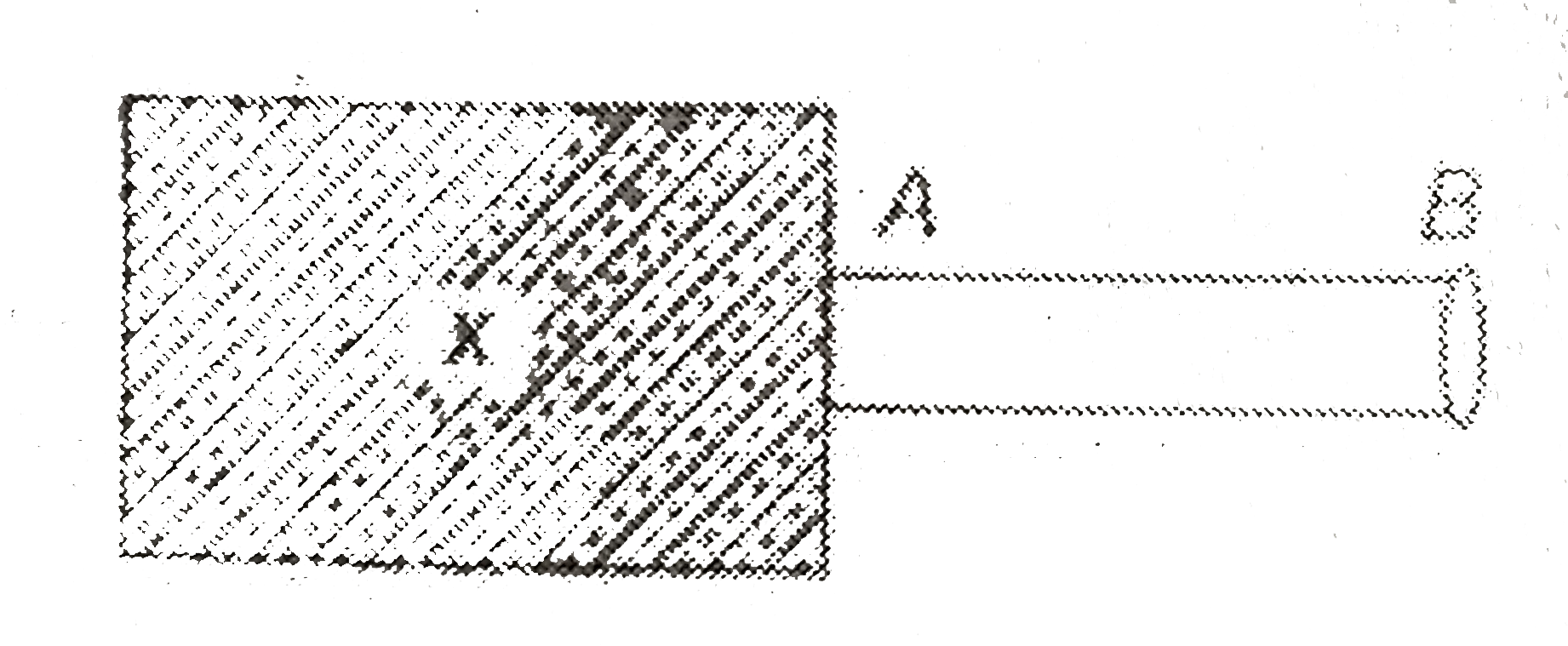
14400 K
12600 K
13000 K
12000 K
The correct Answer is:A
Step by step video, text & image solution for A solid body X of very large heat capacity is kept in an atmosphere whose temperature is 300 K. The body X is connected to a rod of length 1 m and cross sectional area S, as shown in the figure. Thermal conductivity of rod AB is 0.0567W//mK. Assuming that there is no heat exchange with the surrounding except fom the end B of the rod i.e., neither by any surface of X nor by the curved surface of rod. The end B has emissivity e=0.8. If the steady state temperature of the end B is 400 K then find the temperature of X in steady state. (Stefan constant sigma-5.67xx10^(-8)W//m^(2)K^(4)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View Solution" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View Solution
Knowledge Check
Two rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
A(5/6)KB1.5KC1.2KD(8/9)KA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
ALKABKLLCKALDAKLA heat flux of 4000 J/s is to be passed through a copper rod of length 10 cm and area of cross section 100cm2. The thermal conductivity of copper is 400W/m/∘C The two ends of this rod must be kept at a temperature difference of
A1∘CB10∘CC100∘CD1000∘C
Find the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View SolutionWhen two bodies ofmasses m1 and m2 with specific heats s1 and s2 at absolute temperatures T10 and T20(T10>T20) are connected by a rod of length l and cross sectional area A with thermal conductivity k. Find the temperature difference of the bodies after time t. Neglect any heat loss due to radiation at any surface..

View SolutionA heat flux of 4000 J/s is to be passed through a copper rod of length 10 cm and area of cross-section 100 cm. sq. The thermal conductivity of copper is 400 W/mC. The two ends of this rod must be kept at a temperature difference of-
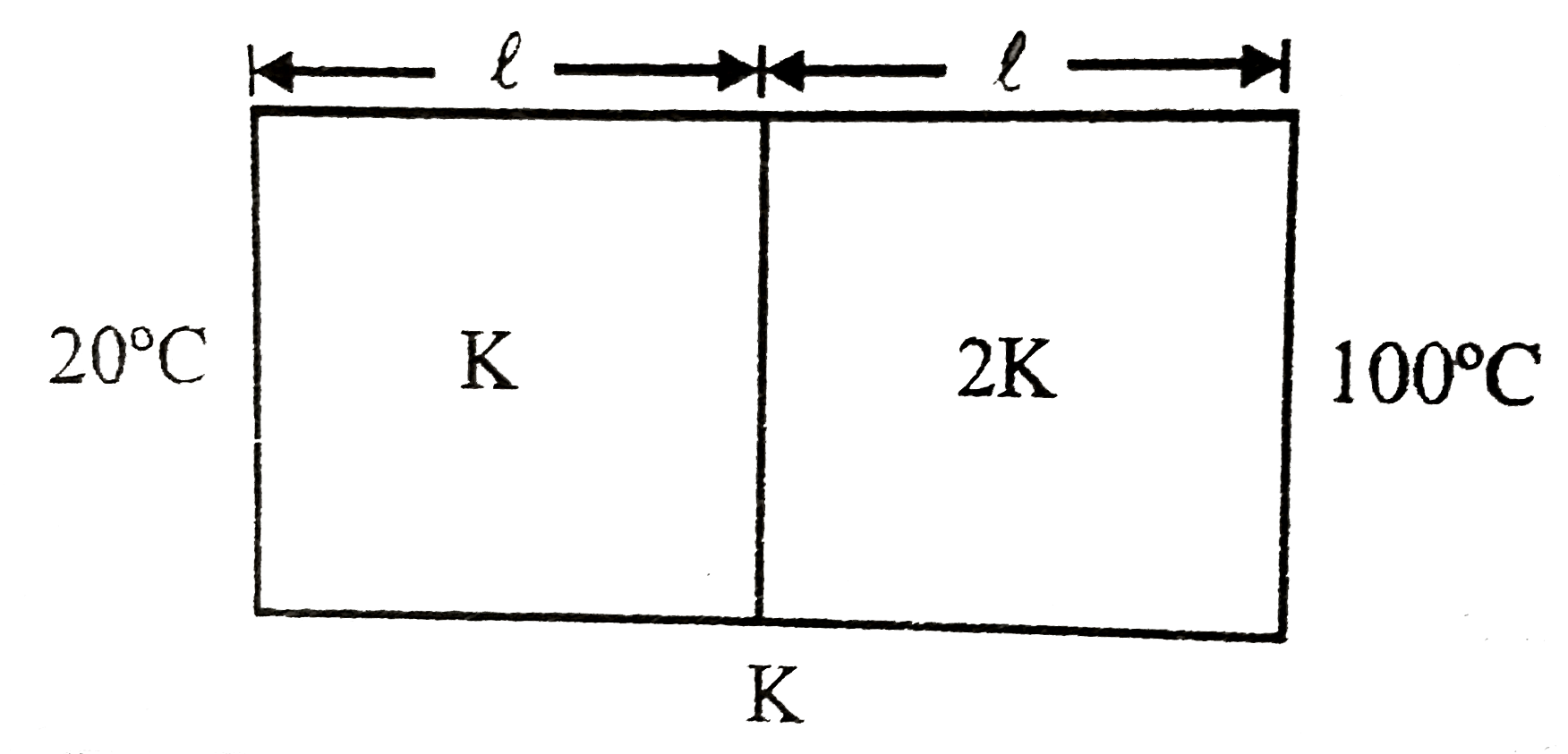
View SolutionTwo rods are connected as shown. The rods are of same length and same cross sectional area. In steady state, the temperature (θ) of the interface will be -
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View Solution
