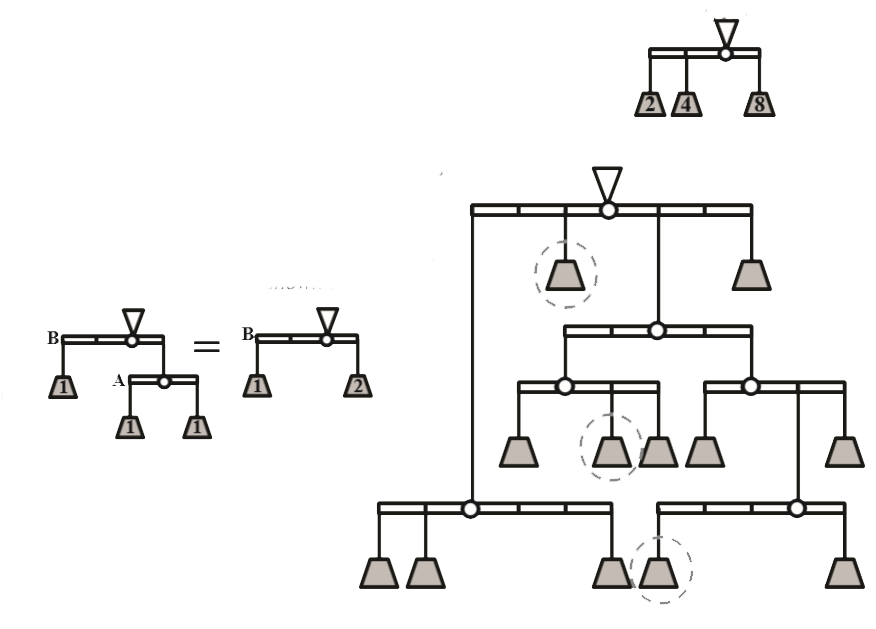
Al Capone loved balances. He took Tintin to his famous room of Balance, where there was present a huge complex balance as shown in the fig_1. The marks on the stick are at 1 metre distance each and the white small circles represent the point around which the stick is hinged. There are 12 identical looking weights which weigh 1kg, 2kg, 3kg,….. upto 12kg. He asked Tintin to identify the weight of each of the weights given that the system is balanced. Tintin identified 9 of them correctly except the encircled ones, can you help him find the rest by telling the sum of the weights of the encircled ones? For balancing the total system all the sticks that hold the weights need to be balanced in themselves. For each of the sticks being balanced the following condition need to be satisfied –
BALANCING of TORQUE : The sum of the products of weight with distance from the hinge on the left side of the hinge should be equal to that on the right side for every rod. Eg. In the system shown beside Torque on the left side=(4kg)x(1m)+(2kg)x(2m)=8kg−m Torque on the right side=(8kg)x(1m)=8kg−m
Also if a stick A is connected below another stick B directly at a given distance d then we can consider the stick A as a weight connected to stick B at the same distance d whose weight is equal to the sum of weights connected to stick A. (as shown below)
17
18
19
20
The answer is
10 9
11 7 2 12 4
5 8 1 6 3
Similar Questions
Knowledge Check
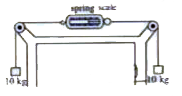
As shown in the figure, two equal masses each of 2kg are suspended from a spring balance. The reading of the spring balance will be.
 AZeroB2kgC4kgDBetween zero and 2kg
AZeroB2kgC4kgDBetween zero and 2kgA metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on of the other at the 12 cm mark, the stick is found to balanced at 45 cm. The mass of the metre stick is:
A56 gB66 gC76 gD36 g
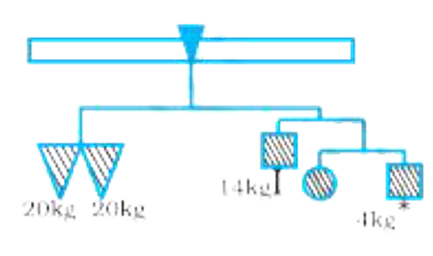
The given figure represents a weighing balance. The weights of some objects in the balance are given. Find the weight of each square and the circle .
View SolutionA metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12 cm mark, the stick is found to be balanced at 45 cm. The mass of metre stick is
View SolutionA metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12 cm mark, the stick is found to be balanced at 45 cm. The mass of metre stick is
View SolutionThe weights of three boxes are 3 kg, 8 kg and 12 kg. Which of the following CANNOT be the total weight, in kg, of any combination of these boxes?
View SolutionA student took a spring balance calibrated in gf. He then suspended an object of mass 1 kg to the spring balance. Determine what would be the reading of the spring balance.
View SolutionA metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5g are put one on of the other at the 12cm mark, the stick is found to balanced at 45cm. The mass of the metre stick is.
View Solution