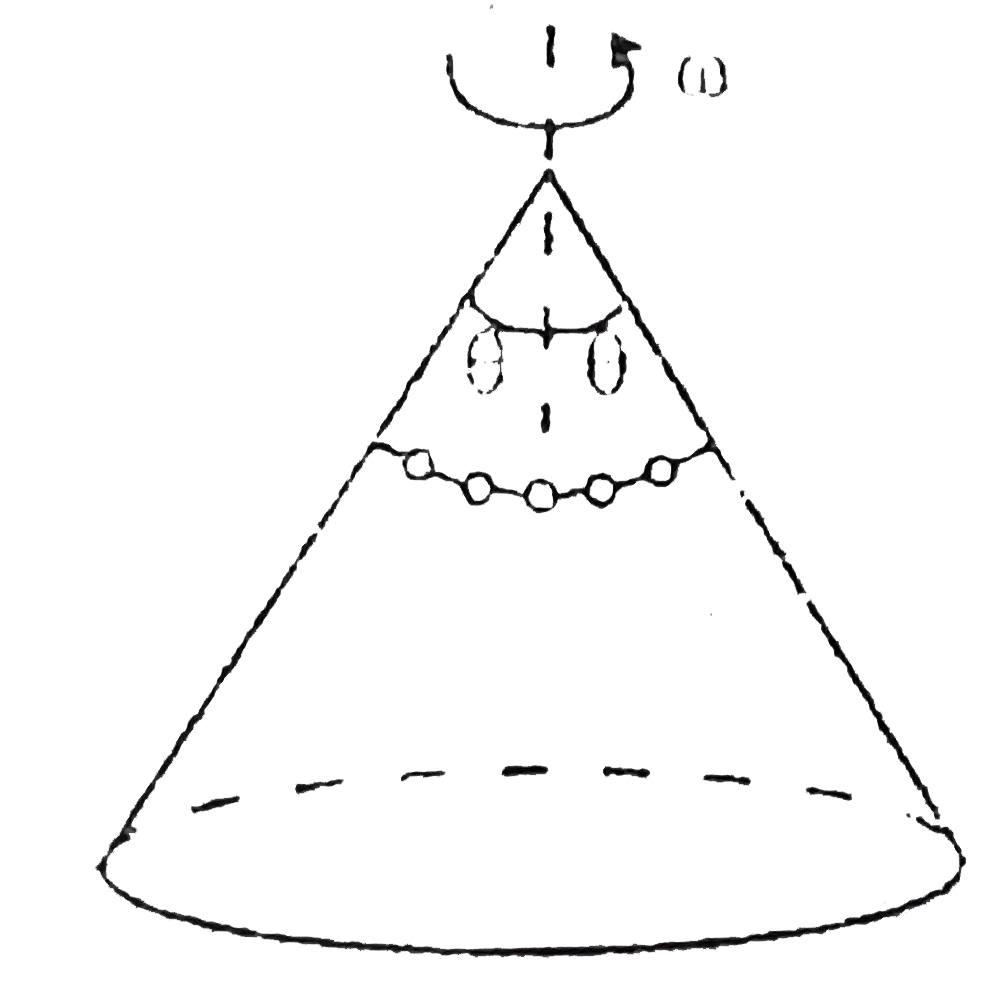
A chain of mass m forming a circle of radius R is slipped on a smooth round cone with half- angle . Find the tension in the chain if it rotates with a constant angular velocity about a vertical axis coinciding with the symmetry axis of the cone .
The correct Answer is:A
To solve the problem of finding the tension in a chain of mass m forming a circle of radius R that is slipped on a smooth cone with half-angle θ, we can follow these steps:
Step 1: Analyze the System
Consider a small element of the chain with mass dm. The chain is rotating with a constant angular velocity ω about the vertical axis of the cone. The gravitational force acting on this element is dm⋅g, where g is the acceleration due to gravity.
Hint: Identify the forces acting on the small mass element of the chain.
Step 2: Identify Forces Acting on the Element
The forces acting on the small element dm are:
1. The weight dm⋅g acting downward.
2. The tension T in the chain acting along the chain.
3. The normal force N acting perpendicular to the surface of the cone.
Step 3: Resolve Forces
Resolve the normal force N into components:
- The vertical component is Ncosθ.
- The horizontal component is Nsinθ.
For the element to be in equilibrium in the vertical direction:
Ncosθ=dm⋅g
For the horizontal direction, the centripetal force required for circular motion is provided by the horizontal component of the normal force and the tension:
Nsinθ+T=dm⋅ω2R
Step 4: Express dm
The mass element dm can be expressed in terms of the total mass m and the angle dα subtended by the element at the center:
dm=m2πdα
Step 5: Substitute dm into the Equations
Substituting dm into the vertical force equation:
Ncosθ=m2πdα⋅g
From this, we can express N:
N=mgdα2πcosθ
Substituting N into the horizontal force equation:
mgdα2πcosθsinθ+T=m2πdα⋅ω2R
Step 6: Isolate Tension T
Rearranging the equation to solve for T:
T=m2πdα⋅ω2R−mgdα2πcosθsinθ
Factoring out mdα2π:
T=mdα2π(ω2R−gsinθcosθ)
Step 7: Simplify the Expression
Using the identity tanθ=sinθcosθ:
T=mdα2π(ω2R−gtanθ)
Final Result
The tension in the chain is given by:
T=m2π(ω2R−gtanθ)
Consider a small element of the chain with mass dm. The chain is rotating with a constant angular velocity ω about the vertical axis of the cone. The gravitational force acting on this element is dm⋅g, where g is the acceleration due to gravity.
The forces acting on the small element dm are:
1. The weight dm⋅g acting downward.
2. The tension T in the chain acting along the chain.
3. The normal force N acting perpendicular to the surface of the cone.
Resolve the normal force N into components:
- The vertical component is Ncosθ.
- The horizontal component is Nsinθ.
Ncosθ=dm⋅g
Nsinθ+T=dm⋅ω2R
The mass element dm can be expressed in terms of the total mass m and the angle dα subtended by the element at the center:
dm=m2πdα
Substituting dm into the vertical force equation:
Ncosθ=m2πdα⋅g
From this, we can express N:
N=mgdα2πcosθ
mgdα2πcosθsinθ+T=m2πdα⋅ω2R
Rearranging the equation to solve for T:
T=m2πdα⋅ω2R−mgdα2πcosθsinθ
Factoring out mdα2π:
T=mdα2π(ω2R−gsinθcosθ)
Using the identity tanθ=sinθcosθ:
T=mdα2π(ω2R−gtanθ)
The tension in the chain is given by:
T=m2π(ω2R−gtanθ)
Topper's Solved these Questions
Similar Questions
A chain of mass m and radius R placed on a smooth table is revolving with a speed v about a vertical axis coinciding with the symmetry axis of the chain. Find the tension in the chain.
View SolutionA sleeve A can slide freely along a smooth rod bent in the shape of a half circle of radius R .The system is set in rotaion with a constant angular velocity ω about a vertical axis OO' .Find the angle θ corresponding to the steady position of the sleeve

View Solution
Knowledge Check
A rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)A rope of mass'm' is looped in a circle of radius R and rotated with a constant angular velocity about its axis in gravity free space . Find the tension in the rope ?
AT=mRω20B2mRπω2CT=mRπω202πD4mRπω20
A chain of mass 'm' and radius 'r' is placed onto a cone of semi vertical angle θ. Cone rotated with angular velocity ω. Find the tension in the chain if it does not slide on the cone.
View SolutionA sleeve A can slide freely along a smooth rod bent in the shape of a half-circle of radius R(figure). The system is set in rotation with a constant angular velocity ω about a vertical axis OO′. Find the angle θ corresponding to the steady position of the sleeve.
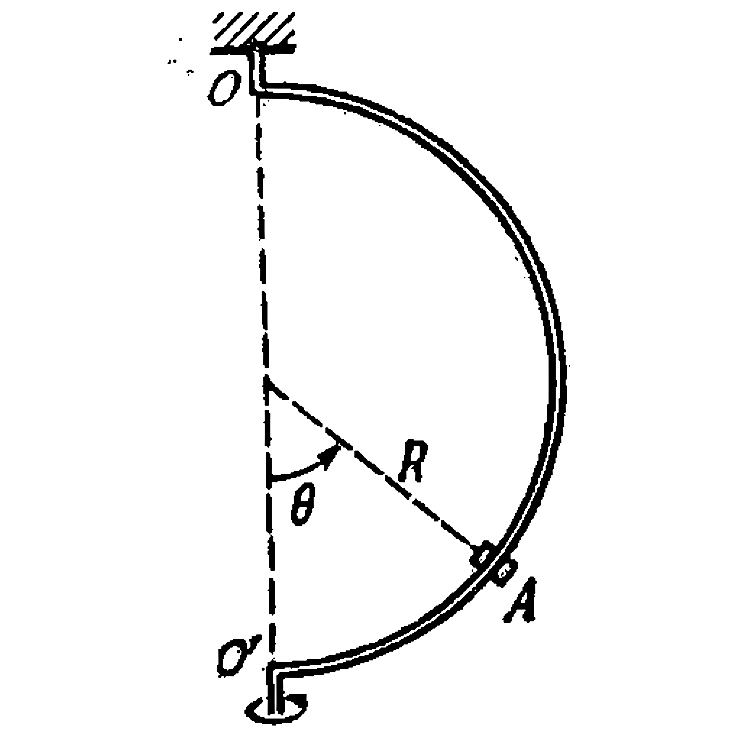
View SolutionFind total energy of the inclined rod of mass m shown in figure-5.39 , rotating with angular velocity ω , about a vertical axis XX', shown in figure .

View SolutionA ring of mass m and radius R is being rotated about its axis with constant angular velocity ω in the gravity free space. Find tension in the ring.
View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
View Solution
