One mole of a diatomic gas undergoes a thermodynamic process, whose process equation is P∝V2. The molar specific heat of the gas is
17R3
17R6
15R4
15R8
The correct Answer is:B
To solve the problem, we need to determine the molar specific heat of one mole of a diatomic gas undergoing a thermodynamic process described by the equation P∝V2. Here are the steps to arrive at the solution:
Step 1: Understand the given relationship
The relationship given is P∝V2. This can be expressed mathematically as:
P=CV2
where C is a constant.
Step 2: Identify the type of process
The equation PVn=constant represents a polytropic process, where n is the polytropic index. From our equation P=CV2, we can rearrange it to fit the polytropic form:
PV−2=C
This indicates that n=−2.
Step 3: Use the formula for molar specific heat in a polytropic process
The formula for the molar specific heat C in a polytropic process is given by:
C=Cb+R1−n
where:
- Cb is the molar specific heat at constant volume,
- R is the universal gas constant,
- n is the polytropic index.
Step 4: Determine Cb for a diatomic gas
For a diatomic gas, the value of Cb is:
Cb=5R2
Step 5: Substitute the values into the formula
Now we can substitute Cb and n into the specific heat formula:
C=5R2+R1−(−2)
This simplifies to:
C=5R2+R1+2=5R2+R3
Step 6: Find a common denominator and simplify
To add these fractions, we need a common denominator. The least common multiple of 2 and 3 is 6:
C=15R6+2R6=17R6
Final Answer
Thus, the molar specific heat of the diatomic gas during this process is:
C=17R6
The relationship given is P∝V2. This can be expressed mathematically as:
P=CV2
where C is a constant.
The equation PVn=constant represents a polytropic process, where n is the polytropic index. From our equation P=CV2, we can rearrange it to fit the polytropic form:
PV−2=C
This indicates that n=−2.
The formula for the molar specific heat C in a polytropic process is given by:
C=Cb+R1−n
where:
- Cb is the molar specific heat at constant volume,
- R is the universal gas constant,
- n is the polytropic index.
For a diatomic gas, the value of Cb is:
Cb=5R2
Now we can substitute Cb and n into the specific heat formula:
C=5R2+R1−(−2)
This simplifies to:
C=5R2+R1+2=5R2+R3
To add these fractions, we need a common denominator. The least common multiple of 2 and 3 is 6:
C=15R6+2R6=17R6
Thus, the molar specific heat of the diatomic gas during this process is:
C=17R6
Topper's Solved these Questions
Similar Questions
One mole of a diatomic gas is taken through the process P/T^(n)=K where n and K are constants.If the molar specific heat of the gas is C=-R/2 then the value of n is
View SolutionOne mole of an ideal monatomic gas undergoes the process P=αT1/2, where α is constant . If molar heat capacity of the gas is βR1 when R = gas constant then find the value of β.
View Solution
Knowledge Check
One mole of an ideal monoatomic gas undergoes a process as shown in the figure. Find the molar specific heat of the gas in the process.
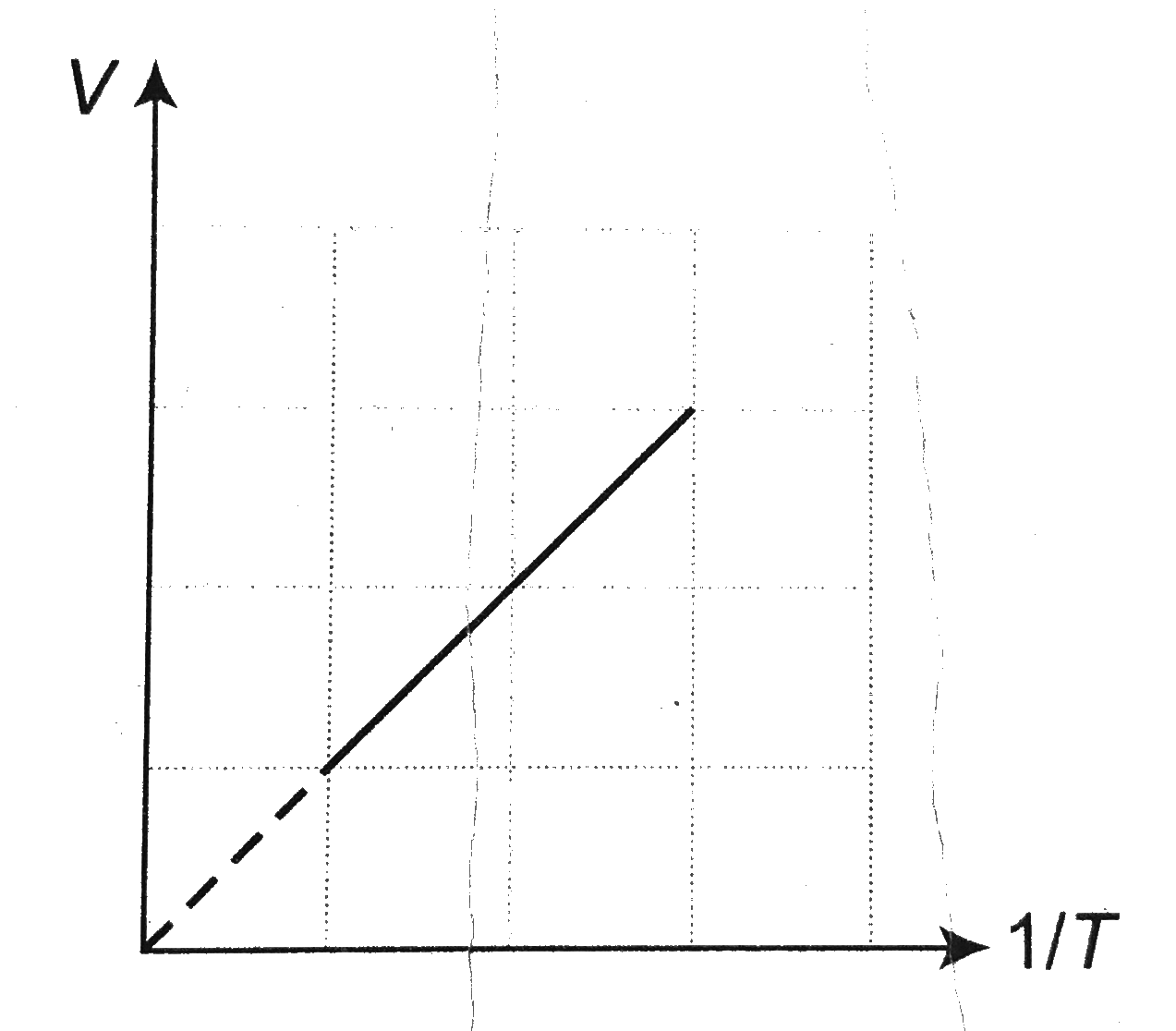
R is a gas constant.A3R4BR2CR3D2R3One mole of a monoatomic ideal gas undergoes a thermodynamic process such thatV3T2= constant. Then,
Awork done by the gas is 200R when temperature of the gas is raised by 300 KBthe specific heat of the gas in the process is 136RCwork done by the gas is 300R when temperature of the gas maised by 600 KDthe specific heat of the gas in the process is 214 ROne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
A32RB52RC2 RDR
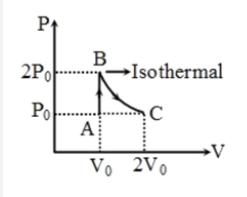
An ideal diatomic gas undergoes a thermodynamic process as shown in the P−V diagram. The process AB is isochoric while the process BC is isothermal. The total heat gain to the gas in the process is nearly (use ln2=0.7)
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3 = constant. The heat capacity of the gas during this process is
View SolutionOne mole of an ideal monatomic gas undergoes a process described by the equation PV3= constant. The heat capacity of the gas during this process is
View SolutionTwo moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The equation of process is
View SolutionA certain amount of ideal monoatomic gas undergoes a process given by TV1/2= constant. The molar specific heat of the gas for the process will be given by
View Solution
