(##COLBODSATPT04_E03013_Q01.png width=80%><br>Thefunction f and g ,def∈edby f (x) = 8x ^ 2 - 2 and g (x) = -8 x ^ 2 + 2 ,aregraphed∈thexy−pla≠above.Thegraphsof f and g ∫ersectatthep∮s ( k, 0 ) and ( -k, 0) .Wˆisthevalueofk ?
14
12
1
2
The correct Answer is:B
To find the value of k where the functions f(x)=8x2−2 and g(x)=−8x2+2 intersect, we need to set the two functions equal to each other and solve for x.
1. Set the functions equal to each other:
f(x)=g(x)
This gives us:
8x2−2=−8x2+2
2. Rearrange the equation:
Add 8x2 to both sides and add 2 to both sides:
8x2+8x2=2+2
This simplifies to:
16x2=4
3. Divide both sides by 16:
x2=416
Simplifying gives:
x2=14
4. Take the square root of both sides:
x=±√14=±12
5. Identify the points of intersection:
The points of intersection are (12,0) and (−12,0).
6. Determine the value of k:
From the points of intersection, we can see that k=12.
Final Answer:
k=12
f(x)=g(x)
This gives us:
8x2−2=−8x2+2
Add 8x2 to both sides and add 2 to both sides:
8x2+8x2=2+2
This simplifies to:
16x2=4
x2=416
Simplifying gives:
x2=14
x=±√14=±12
The points of intersection are (12,0) and (−12,0).
From the points of intersection, we can see that k=12.
k=12
Similar Questions
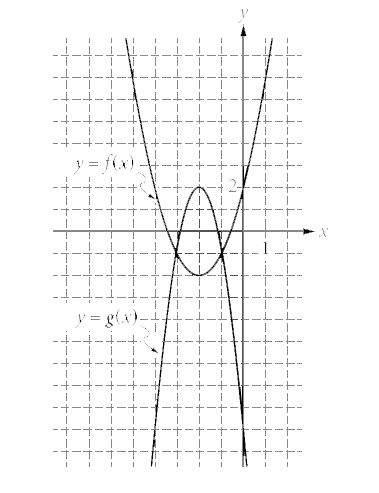
Graphs of the functions f and g are shown in the xy-plane above. For which of the following values of x does f(x)+g(x)=0 ?
View Solutionf(x)=2x+1
The function f is defined by the equation above which of the following is the graph of y=−f(x) in the xy-plane?
View SolutionIf g(x)=2x2+3x−4 and g(f(x))=8x2+14x+1 then f (2) =
View Solutionf,g వాస్తవ మూల్య ప్రమేయాలను f(x)=2x−1,g(x)=x2 గా నిర్వచిస్తే , కింది వాటిని కనుక్కోండి. (f + g + 2 )(x)
View SolutionIf f (x) is a function such that f''(x)+f(x)=0 and g(x)=[f(x)]2+[f'(x)]2 and g(3)=3 then g(8)=
View SolutionIf g(x)=2x2+3x−4 and g(f(x))=8x2+14x+1 then f (2) =
View SolutionIf f(x) is a function such that f(x)+f''(x)=0andg(x)=(f(x))2+(f'(x))2andg(3)=8, then g(8)=
View Solution
