Line l in the xy-plane contains points from each of Quadrants II, III, and IV, but no points from Quadrant I. Which of the following must be true?
The slope of line l is undefined.
The slope of line l is zero.
The slope of line l is positive.
The slope of line l is negative.
The correct Answer is:D
To solve the problem, we need to analyze the characteristics of line l in the xy-plane that passes through Quadrants II, III, and IV but does not intersect Quadrant I.
1. Understanding the Quadrants:
- The xy-plane is divided into four quadrants:
- Quadrant I: (x>0,y>0)
- Quadrant II: (x<0,y>0)
- Quadrant III: (x<0,y<0)
- Quadrant IV: (x>0,y<0)
2. Identifying the Line's Position:
- Since the line contains points from Quadrants II, III, and IV, it must extend from the left side of the y-axis (Quadrant II) to the right side of the x-axis (Quadrant IV).
- The line cannot enter Quadrant I, which means it must either be horizontal or have a negative slope.
3. Slope Calculation:
- The slope m of a line is defined as the change in y divided by the change in x (i.e., m=ΔyΔx).
- To illustrate this, we can take two points on the line:
- Point A in Quadrant II: (−2,4)
- Point B in Quadrant IV: (2,−4)
4. Calculating the Slope:
- Using the two points, we calculate the slope:
m=y2−y1x2−x1=−4−42−(−2)=−84=−2
- The slope is negative, which confirms that the line is decreasing as it moves from Quadrant II to Quadrant IV.
5. Conclusion:
- Since the line has a negative slope and passes through Quadrants II, III, and IV but not Quadrant I, we can conclude that the statement about the slope being negative must be true.
Final Answer:
The slope of the line l is negative.
- The xy-plane is divided into four quadrants:
- Quadrant I: (x>0,y>0)
- Quadrant II: (x<0,y>0)
- Quadrant III: (x<0,y<0)
- Quadrant IV: (x>0,y<0)
- Since the line contains points from Quadrants II, III, and IV, it must extend from the left side of the y-axis (Quadrant II) to the right side of the x-axis (Quadrant IV).
- The line cannot enter Quadrant I, which means it must either be horizontal or have a negative slope.
- The slope m of a line is defined as the change in y divided by the change in x (i.e., m=ΔyΔx).
- To illustrate this, we can take two points on the line:
- Point A in Quadrant II: (−2,4)
- Point B in Quadrant IV: (2,−4)
- Using the two points, we calculate the slope:
m=y2−y1x2−x1=−4−42−(−2)=−84=−2
- The slope is negative, which confirms that the line is decreasing as it moves from Quadrant II to Quadrant IV.
- Since the line has a negative slope and passes through Quadrants II, III, and IV but not Quadrant I, we can conclude that the statement about the slope being negative must be true.
The slope of the line l is negative.
Similar Questions
Knowledge Check
From the figure, which one of the following must be true?
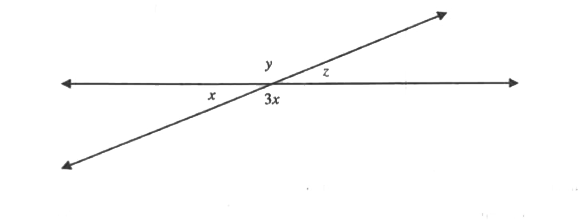 Ay=zBy<zCy≤zDy>z
Ay=zBy<zCy≤zDy>zIn the figure, line l and k are parallel. Which one of the following must be true?
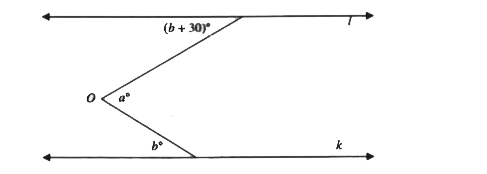 Aa lt bBa≤bCa=bDa>b
Aa lt bBa≤bCa=bDa>bOn the number line, the distance between the point whose coordinate is s and the point whose coordinate is t is greater than 500. Which of the following must be true?
I. |s|.|t|>500
II. |s−t|>500
III. t−s>500AI onlyBII onlyCI and II onlyDI, II, and III
In which quadrant do the following points lies: (0,−5)
View SolutionA line contains the points A,B,C and D. Point B is between points A and C. Point D is between points C and B. Which of the following inequalities must be true about lengths of these segments?
View SolutionIf the point (a,b) is in Quadrant II and |a|−|b|>0, then which one of the following is true?
View SolutionLine m in the xy-plane contains the points (2, 4) and (0, 1).Which of the following is an equation of line m ?
View SolutionIf the line y=3x−15 intersects the line y=mx+8 in the third quadrant, which of the follwing must be true ?
View Solution
