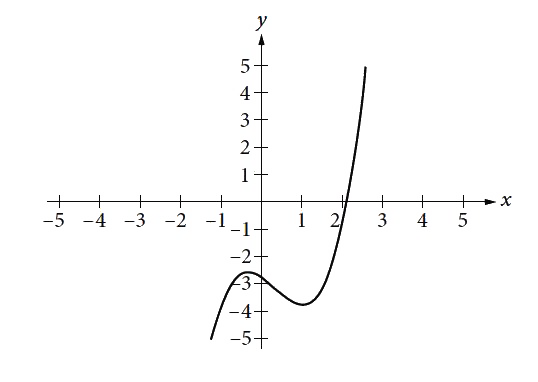
The function $f (x) = x^{3} - x^{2} - x - \frac{11}{4}$ s graphed in the xy-plane above. If k is a constant such that the equation f(x)=k has three real solutions, which of the following could be the value of k ?

A

2

B

0

C

$- 2$

D

$- 3$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

The equation f(x) = k gives the solutions to the system of equations $y = f (x) = x^{3} - x^{2} - x - 141$ and y = k. A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the xy-plane. The graph of y = k is a horizontal line that contains the point (0, k). Thus, the line with equation y = −3 is a horizontal line that intersects the graph of the cubic equation three times, and it follows that the equation f(x) = −3 has three real solutions.
Choices A, B, and C are incorrect because the graphs of the corresponding equations are horizontal lines that do not intersect the graph of the cubic equation three times.

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Question 1 - Select One
$2 x^{2} - 4 x = t$
In the equation above, t is a constant. If the equation has no real solutions, which of the following could be the value of t ?
A $- 3$
B $- 1$
C $1$
D3
Question 2 - Select One

If $g (x) = - 2$ intersects the graph of $y = f (x) + k$ at one point, which of these choices could be the value of k?
A $- 1.5$
B $- 0.5$
C $0$
D $1.5$
Question 3 - Select One

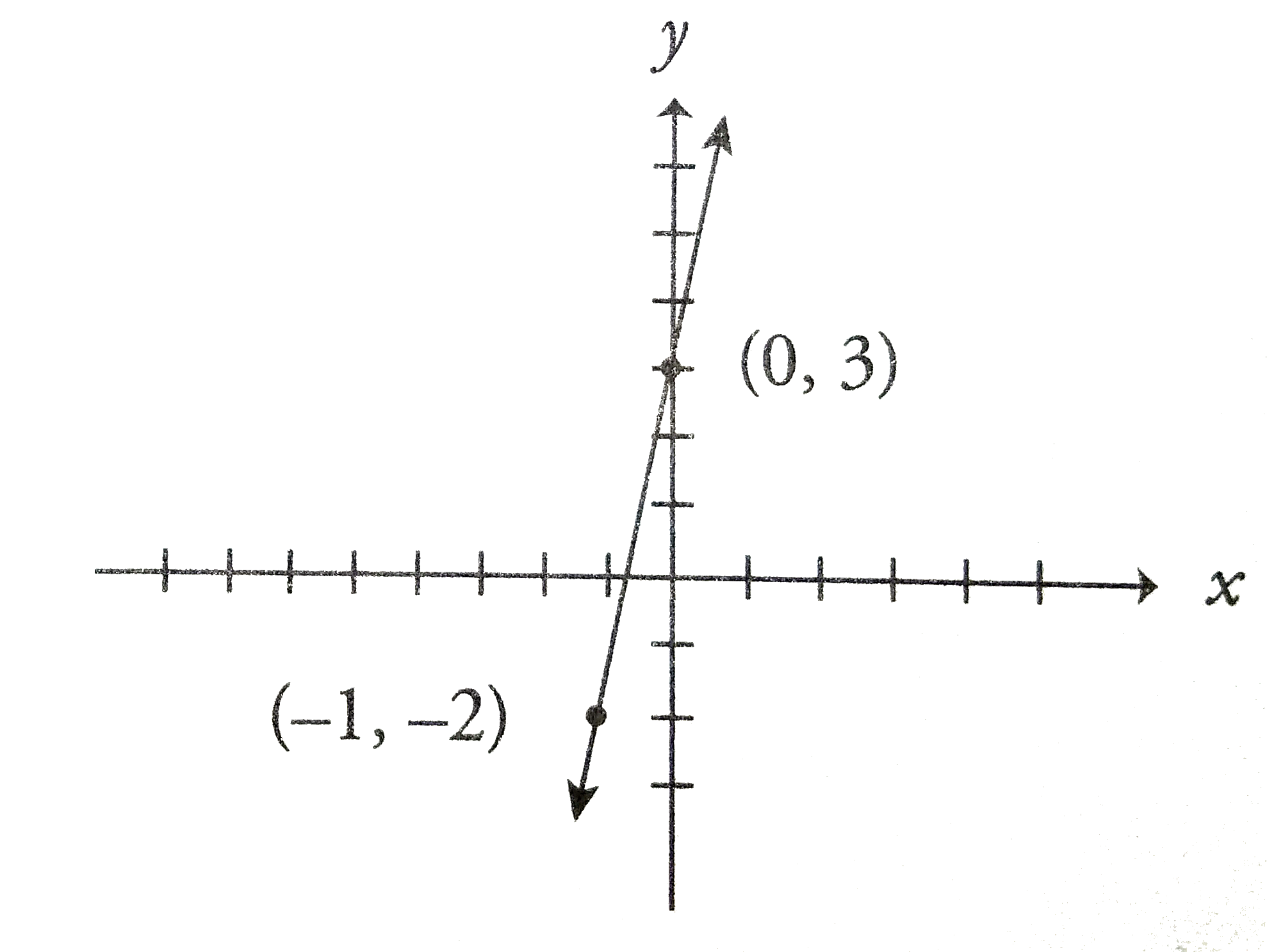
If the graph above is that of f(x), which of the following could be f(x)?
A $f (x) = \frac{1}{5} x + \frac{1}{5}$
B $f (x) = \frac{1}{5} x + 3$
C $f (x) = 3 x + 5$
D $f (x) = 5 x + 3$

Recommended Questions

Home
Ask Doubt
Profile