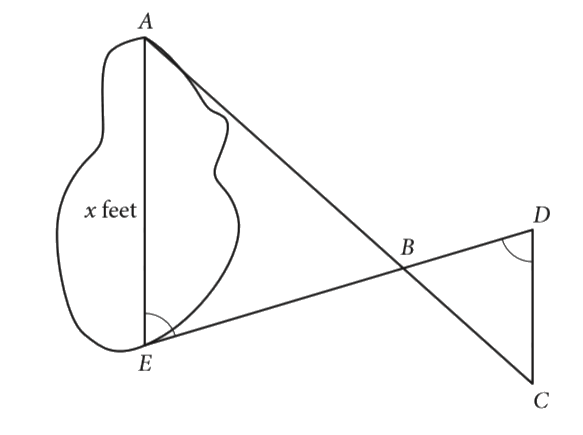
A summer camp counselor wants to find a length, x, in feet, across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet, and 800 feet, respectively. Segments AC and DE intersect at B, and ∠AEB and ∠CDB have the same measure. What is the value of x ?
Text Solution
The correct Answer is:1600
|
Similar Questions

A scientist looking at a sample of infected tissue through a microscope wants to find the length x, in mircos, across a damaged blood cell, as represented in the sketch above. The lengths represented by AB, EB, BD, and CD were determined to be 26 microns, 22 microns, 11 microns, and 12 microns, respectively. Given that the measure of ∠AEB is equal to the measure of ∠CDB, what is the value of x?

View SolutionA gardener has a cultivated plot that measures 4 feet by 6 feet. Next year, she wants to double the area of her plot by increasing the length and width by x feet. What is the value of x?
View Solution
Knowledge Check
Pedal Triangle of a Triangle: Let ΔABC be any triangle and let D, E, F be the feet of perpendiculars from the vertices A, B, C on the opposite sides BC, CA, AB respectively, then the triangle DEF is known as Pedal triangle of ABC. H is the orthocentre of the ΔABC. We note that ∠HDC=∠HEC=90∘'
∴∠HDE=∠HCE=90∘−A.
Simillarly ∠HDF=∠HBF=90∘−A.
Hence, ∠FDE=180∘−2A.
Identically we can find ∠DEF=180∘−2B
and ∠EFD=180∘−2C.
Thus, the angles of Pedal triangle are 180∘−2A,180∘−2B,180∘−2C. Further in ΔBFD,∠FDB=90∘−(90∘−A)=A, thus FBsinB=FBsinA
∴FD=sinBsinA(BCcosB)=asinBcosBsinA=2RsinBcosB=bcosB.
Similarly, EF=acosAandDE=ccosC.
Thus, the sides of pedal triangle are acosA,bcosBandccosC(orRsin2A,Rsin2B,Rsin2C), where R is the circumradius of ΔABC.
In the above derivation, the triangle ABC is assumed an acute angled triangle. In case the triangle ABC be obtuse angled with A as obtuse angle, then, the angles of pedal triangle will be represented by 2A−180∘,2B,2Cand the sides will be represented by −acosA,bcosB,ccosC.
The inradius of the pedal triangle of a tringle ABC isAR/2BRsinA2sinB2sinC2C2RcosAcosBcosCD4RsinA2sinB2sinC2
