Jessica opened a bank account that earns 2 percent interest compounded annually. Her initial deposit was $100, and she uses the expression $100(x)t to find the value of the account after t years.
Jessica’s friend Tyshaun found an account that earns 2.5 percent interest compounded annually. Tyshaun made an initial deposit of $100 into this account at the same time Jessica made a deposit of $100 into her account. After 10 years, how much more money will Tyshaun’s initial deposit have earned than Jessica’s initial deposit? (Round your answer to the nearest cent and ignore the dollar sign when gridding your response.)
To solve the problem, we need to calculate the future values of both Jessica's and Tyshaun's bank accounts after 10 years and then find the difference between the two amounts.
Step 1: Calculate the future value of Jessica's account
Jessica's account earns 2% interest compounded annually. The formula for the future value (F) of an investment compounded annually is given by:
F=A×(1+r)t
Where:
- A = initial deposit
- r = annual interest rate (in decimal)
- t = number of years
For Jessica:
- A=100
- r=2%=0.02
- t=10
Substituting the values into the formula:
FJ=100×(1+0.02)10
Calculating 1+0.02:
FJ=100×(1.02)10
Now we calculate (1.02)10:
(1.02)10≈1.21899
Now, substituting this back into the formula:
FJ≈100×1.21899≈121.90
Step 2: Calculate the future value of Tyshaun's account
Tyshaun's account earns 2.5% interest compounded annually. Using the same formula:
For Tyshaun:
- A=100
- r=2.5%=0.025
- t=10
Substituting the values into the formula:
FT=100×(1+0.025)10
Calculating 1+0.025:
FT=100×(1.025)10
Now we calculate (1.025)10:
(1.025)10≈1.28008
Now, substituting this back into the formula:
FT≈100×1.28008≈128.01
Step 3: Find the difference between Tyshaun's and Jessica's account values
Now we subtract the future value of Jessica's account from Tyshaun's account:
Difference=FT−FJ
Substituting the values we calculated:
Difference≈128.01−121.90≈6.11
Final Answer
The amount Tyshaun's initial deposit has earned more than Jessica's initial deposit after 10 years is approximately 6.11.
---
Jessica's account earns 2% interest compounded annually. The formula for the future value (F) of an investment compounded annually is given by:
- A = initial deposit
- r = annual interest rate (in decimal)
- t = number of years
- A=100
- r=2%=0.02
- t=10
Tyshaun's account earns 2.5% interest compounded annually. Using the same formula:
- A=100
- r=2.5%=0.025
- t=10
Now we subtract the future value of Jessica's account from Tyshaun's account:
The amount Tyshaun's initial deposit has earned more than Jessica's initial deposit after 10 years is approximately 6.11.
Similar Questions
Jessica opened a bank account that earns 2 percent interest compounded annually. Her initial deposit was $100, and she uses the expression $100(x)t to find the value of the account after t years.
What is the value of x in the expression?
View SolutionAt a certain bank, month held in account X earns a monthly interest equal to 2 percent of the original investment, while account Y earns a monthly interest equal to 2 reprecent of the current value of the account. If $500 is invested into each account, what is the positive difference between the value of account X and account Y after three years ? (Round you answer to the nearest dollar and ignore the dollar sign when gridding you response.)
View Solution
Knowledge Check
A bank account pays interest at an annual rate of 4%. If the initial deposit on the account is $1,250 and no other deposits or withdrawals are made to the account, which of the following functions A models the account of money in the bank account after y years?
AA(y)=0.04(1,250)yBA(y)=1.04(1,250)yCA(y)=1,250(0.04)yDA(y)=1,250(1.04)yBecca deposits $100 into a bank account that earns an annual interest rate of 4%. If she does not make any additional deposits and makes no withdrawals, how long will it take her, in years, to increase the value of her account by at least 60%?
A12B15C25D30
a=18t+15
Jane made an initial deposit to a savings account. Each week thereafter she deposited a fixed amount to the account. The equation above models the amount a, in dollars, that Jane has deposited after t weekly deposits. According to the model, how many dollars was Jane’s initial deposit? (Disregard the $ sign when gridding your answer.)
View SolutionSasha invested $1,200 in a savings account at an annual interest rate of 1.6% compounded annually. She made no further deposits or withdrawals. To the nearest dollar, how much more money did she have in the account after 3 years than after 2 years?
View SolutionLori deposists $100 in a savings account at 2% interest, compounded annually. After three years, what is the balance on the account? (Assume Lori makes no withdrawals or deposits.)
View SolutionA person places Rs 500 in an account that interest compounded continuously. Assuming no additional deposits or withdrawals, how much will be in the account after seven years if the interest rate isa constant 8.5 percent for the first four year and a constant 9.25 percent for the last three years
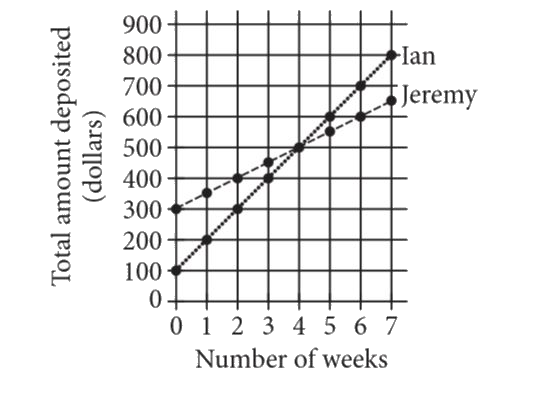
View SolutionThe two graphs above show the total amounts of money that Ian and Jeremy each have deposited into their savings accounts for the first seven weeks after opening their accounts. After they made their initial deposits, how much more did Ian deposit each week than Jeremy?
View SolutionWhat will Rs. 500 amounts to in 10 years after its deposit in a bank which pays annual interest are 10% compounded annually?
View Solution
