The mean score of 8 players in a basketball game was 14.5 points. IF the highest individual score is removed, the mean score of the remaining 7 players becomes 12 points. What was the highest score?
20
24
32
36
To find the highest score among the 8 players, we can follow these steps:
Step 1: Calculate the total score of the 8 players.
Given the mean score of the 8 players is 14.5 points, we can use the formula for mean:
Mean=Total ScoreNumber of Players
So, we can rearrange this to find the total score:
Total Score=Mean×Number of Players
Substituting the values:
Total Score=14.5×8
Calculating this gives:
Total Score=116
Step 2: Calculate the total score of the remaining 7 players.
We know that when the highest score is removed, the mean score of the remaining 7 players becomes 12 points. Again, using the mean formula:
Total Score of 7 Players=Mean×Number of Players
Substituting the values:
Total Score of 7 Players=12×7
Calculating this gives:
Total Score of 7 Players=84
Step 3: Calculate the highest score.
Now we can find the highest score by subtracting the total score of the 7 players from the total score of the 8 players:
Highest Score=Total Score of 8 Players−Total Score of 7 Players
Substituting the values we calculated:
Highest Score=116−84
Calculating this gives:
Highest Score=32
Therefore, the highest score is 32 points.
---
Similar Questions
The total score in a football game was 72 points. The winning team scored 12 points more than the closing team. How many points did the winning team score?
View SolutionIn order to compensate for a diffecult midterm exam. Danialle's mathematics teacher adjusted each of the 25 students' midterm exam scores by replacing it by one half of the original score increased by 50. If the mean of the revised set of midterm scores is 82, what was the mean of the original set of scores?
View Solution
Knowledge Check
Twenty-one people were playing a game. 1 person scored 50 points, 2 people scored 60 points, 3 people scored 70 points, 4 people scored 80 points, 5 people scored 90 points, and 6 people scored 100 points. Which of the following correctly shows the order of the median, mode and average (arithmetic mean) of the 21 scores?
Aaverage<median<modeBaverage<mode<medianCmedian<mole<averageDmedian<average<modeKanaka took 8 tests for her social studies class. Each test has a maximum score of 100 and a minimum score of 0. On the 8 tests, Kanaka's mean score was 90. More than a quarter of her tests have scores less than 85. IF the average of the remaining tests is x, which of the following must be true?
Ax≤85B85<x<90Cx=90Dx>90The lowest value in a set of ordered scores is x and the highest value is y. If each score is increased by k, then which of the following must be true of the revised set of scores?
I. The mean is increased by k.
II. The range is k.
III.The median remains unchanged.AI onlyBII onlyCI and III onlyDII and III only
The mean of 24 test scores is 77.5. When the 25th class member takes the test, the mean down by 1.1 points. What was that 25h score?
View SolutionThe average (arithmetic mean) of 8 numbers is 65. If one of the numbers, 65, removed, what is the average of the remaining 7 numbers?
View SolutionGrace's average bowling score over the past 6 games is 150. If she wants to raise her average score by 10%, and she has two more games remaining in the season, what must her average score on the last two games be ?
View SolutionAt a shooting competition the scores of a competitor were as given below: (i) What was his modal score?
(ii) What was his median score?
(iii) What was his total score? (iv) What was his mean score?
View Solution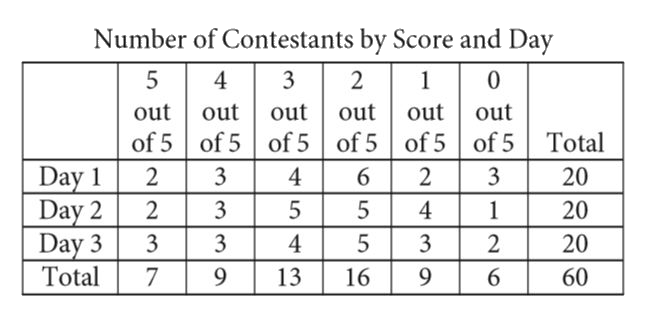
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?
View Solution