In a certain game, each player scores either 2 points or 5 points. If n players score 2 points and m players score 5 points, and the total number of points scored is 50, what is the least possible difference between m and n ? (a) 1 (b) 3 (c) 5 (d) 7
To solve the problem, we need to set up an equation based on the information given.
1. Understanding the Problem:
- Let n be the number of players who scored 2 points.
- Let m be the number of players who scored 5 points.
- The total points scored by all players is 50.
2. Setting Up the Equation:
- The total points scored can be expressed as:
\(
2n + 5m = 50
\)
3. Rearranging the Equation:
- We can rearrange the equation to find a relationship between n and m:
\(
2n = 50 - 5m
\)
\(
n = \frac{50 - 5m}{2}
\)
4. Finding Integer Solutions:
- For n to be an integer, \(50 - 5m\) must be even. Since 50 is even, \(5m\) must also be even. This means m must be even (because 5 is odd, and an odd number times an even number is even).
- Let’s denote m as \(m = 2k\) where \(k\) is an integer.
5. Substituting Back:
- Substitute \(m = 2k\) into the equation for n:
\(
n = \frac{50 - 5(2k)}{2} = \frac{50 - 10k}{2} = 25 - 5k
\)
6. Finding the Difference:
- We need to find the least possible difference between m and n:
\(
|m - n| = |2k - (25 - 5k)| = |2k - 25 + 5k| = |7k - 25|
\)
7. Minimizing the Difference:
- We want to minimize \(|7k - 25|\). This expression will be minimized when \(7k\) is as close to 25 as possible.
- Solving \(7k = 25\) gives \(k \approx 3.57\). The closest integers are \(k = 3\) and \(k = 4\).
8. Calculating for k = 3:
- If \(k = 3\):
\(
m = 2(3) = 6
\)
\(
n = 25 - 5(3) = 10
\)
\(
|m - n| = |6 - 10| = 4
\)
9. Calculating for k = 4:
- If \(k = 4\):
\(
m = 2(4) = 8
\)
\(
n = 25 - 5(4) = 5
\)
\(
|m - n| = |8 - 5| = 3
\)
10. Conclusion:
- The least possible difference between m and n is 3.
Thus, the answer is (b) 3.
- Let n be the number of players who scored 2 points.
- Let m be the number of players who scored 5 points.
- The total points scored by all players is 50.
- The total points scored can be expressed as:
\(
2n + 5m = 50
\)
- We can rearrange the equation to find a relationship between n and m:
\(
2n = 50 - 5m
\)
\(
n = \frac{50 - 5m}{2}
\)
- For n to be an integer, \(50 - 5m\) must be even. Since 50 is even, \(5m\) must also be even. This means m must be even (because 5 is odd, and an odd number times an even number is even).
- Let’s denote m as \(m = 2k\) where \(k\) is an integer.
- Substitute \(m = 2k\) into the equation for n:
\(
n = \frac{50 - 5(2k)}{2} = \frac{50 - 10k}{2} = 25 - 5k
\)
- We need to find the least possible difference between m and n:
\(
|m - n| = |2k - (25 - 5k)| = |2k - 25 + 5k| = |7k - 25|
\)
- We want to minimize \(|7k - 25|\). This expression will be minimized when \(7k\) is as close to 25 as possible.
- Solving \(7k = 25\) gives \(k \approx 3.57\). The closest integers are \(k = 3\) and \(k = 4\).
- If \(k = 3\):
\(
m = 2(3) = 6
\)
\(
n = 25 - 5(3) = 10
\)
\(
|m - n| = |6 - 10| = 4
\)
- If \(k = 4\):
\(
m = 2(4) = 8
\)
\(
n = 25 - 5(4) = 5
\)
\(
|m - n| = |8 - 5| = 3
\)
- The least possible difference between m and n is 3.
Similar Questions
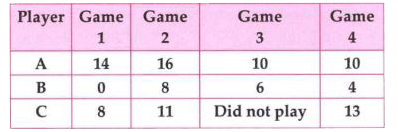
Following table shows the points of each player scored in four games

Now answer the following questions
Find the mean to determine A' s average number of points scored per game
View SolutionIn a game of 100 points , A scores 100 points , while B scores only 75 points .In this game, how many points can A give to B?
View Solution
Knowledge Check
In a game of 100 points ,A scores 100 points while B scores only 65 points .In this game,how much point scan A give to B?
A45B35C25D55
In a basketball match, Jeff scored n points and Bill scored seven points less than Jeff. How many points did Bill score?
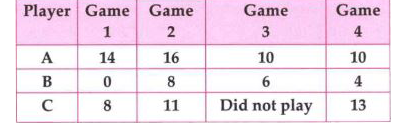
View SolutionFollowing table shows the points of each player scored in four games
Now answer the following questions
To find the mean number of points per game for C, would you divide the total points by 3 or by 4 ? why ?
View SolutionA team of 8 persons joins in a shooting competition. The best marksman scored 85 points. If he had scored 92 points, the average score for the team would have been 84. The number of points, the team scored was (a) 588 (b) 645 (c) 665 (d) 672
View Solution4. In a class of 36 students, 1/3 of the students scored A in mathematics exam,1/2 of them scored B and the rest scored C. Find the numbers of students who scored C in mathematics exam.
View SolutionFollowing table shows the points of each player scored in four games
Now answer the following questions
Who is the best performer ?
View SolutionIn a test, it is possible to have a negative score. If Krishna's score is 15, what is his new score if he loses 20 points?
View SolutionA hockey player scored the following number of goals in 9 matches : 4,3,0,5,2,1,0,1,2. Find th mean of the data.
View Solution
