A stream of a liquid of density p flowin horizontally with speed v rushes out of a tube of radius r and hits a verticla wall nearly normally. Assumi g that the liquid does not rebound from the wall, the force exerted o the wall by the impact of the liquid is given by
πrρv
πrρv2
πr2ρv
πr2ρv2
The correct Answer is:D
To solve the problem of determining the force exerted on a vertical wall by a stream of liquid flowing horizontally, we can follow these steps:
1. Identify the parameters:
- Let the density of the liquid be ρ.
- The speed of the liquid as it exits the tube is v.
- The radius of the tube is r.
2. Calculate the cross-sectional area of the tube:
- The cross-sectional area A of the tube can be calculated using the formula for the area of a circle:
A=πr2
3. Determine the volume flow rate:
- The volume flow rate Q (volume per unit time) of the liquid can be expressed as:
Q=A⋅v=πr2⋅v
4. Calculate the mass flow rate:
- The mass flow rate dmdt can be found using the relationship between mass, density, and volume:
dmdt=ρ⋅Q=ρ⋅(πr2v)=πr2ρv
5. Apply the principle of momentum change:
- When the liquid hits the wall, it comes to a stop (assuming it does not rebound). The change in momentum per unit time (which is the force exerted on the wall) is given by:
F=dPdt=d(mv)dt
- Since the velocity v is constant, we can simplify this to:
F=v⋅dmdt
6. Substitute the mass flow rate into the force equation:
- Now substituting dmdt into the force equation:
F=v⋅(πr2ρv)=πr2ρv2
7. Final expression for the force:
- Thus, the force exerted on the wall by the impact of the liquid is:
F=πr2ρv2
Final Answer:
The force exerted on the wall by the impact of the liquid is given by:
F=πr2ρv2
- Let the density of the liquid be ρ.
- The speed of the liquid as it exits the tube is v.
- The radius of the tube is r.
- The cross-sectional area A of the tube can be calculated using the formula for the area of a circle:
A=πr2
- The volume flow rate Q (volume per unit time) of the liquid can be expressed as:
Q=A⋅v=πr2⋅v
- The mass flow rate dmdt can be found using the relationship between mass, density, and volume:
dmdt=ρ⋅Q=ρ⋅(πr2v)=πr2ρv
- When the liquid hits the wall, it comes to a stop (assuming it does not rebound). The change in momentum per unit time (which is the force exerted on the wall) is given by:
F=dPdt=d(mv)dt
- Since the velocity v is constant, we can simplify this to:
F=v⋅dmdt
- Now substituting dmdt into the force equation:
F=v⋅(πr2ρv)=πr2ρv2
- Thus, the force exerted on the wall by the impact of the liquid is:
F=πr2ρv2
The force exerted on the wall by the impact of the liquid is given by:
F=πr2ρv2
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)
22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(AIIMS)
26 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEYCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
A stream of water flowing horizontal with a speed of 15ms−1 gushes out of tube of cross sectional area 102m2 and hits at a vertical wall nearby . What is the force exerted by the impact of water, assuming that water rebounds with the same speed.
View SolutionTwo non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.

(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
View Solution
Knowledge Check
A steam of water flowing horizontally with a speed of 25ms−1 gushes out of a tube of cross-sectional area 10−3m2, and hits at a vertical wall nearby. What is the force exerted on the wall by the impact of water
A125NB625NC−650ND−1125NA stream of water flowing horizontally with a speed of 15 m/s gushes out of a tube of cross sectional area 10−2m2 and hits at a vertical wall and after collision falls dead. The force exerted on the wall by the impact of water is
A225 NB2250 NC520 NDnone of theseChoose the most appropriate option.
A stream of water flowing horizontally with the speed of 15 ms−2 gushes out of a tube of cross-sectional area 10−2m−2 and hits a vertical wall nearby. What is the force exerted on the wall by the impact or water? Assuming it does not rebound.A2250 NB2000 NC1500 ND1000 N
A stream of water flowing horizontally with a speed of 15ms−1 gushes out of a tube of cross-sectional area 10−2m2, and hits a vertical wall nearby. What is the force exerted on the wall by the impact of water, assuming it does not rebound?
View SolutionA stream of water flowing horizontally with a speed of 15ms−1 pushes out of a tube of cross sectional area 10−2m2 and hits a vertical wall near by what is the force exerted on the wall by the impact of water assuming.that it does not rebound? (Density of water =1000kgm3)
View SolutionA horizontal jet of water coming out of a pipe of area of cross-section 20cm2 hits a vertical wall with a velocity of 10ms−1 and rebounds with the same speed. The force exerted by water on the wall is .
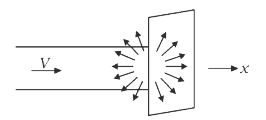
View SolutionA liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
View SolutionA liquid of density ρ comes out with a velocity v from a horizontal tube of area of cross-section A. The reaction force exerted by the liquid on the tube is F :
View Solution
