A cyclist speeding at 6ms−1 in a circle of 18 m radius makes an angle θwith the vertical. Calculate θ. Also determine the minimum possible value of the coefficient of friction between the tyres and the ground?
Given, v=6ms−1,r18m,g=9.8ms−2.
Since, tanθ=v2rg⇒tanθ=6×618×9.8=0.2041
⇒ θ=tan−1(0.2041)⇒θ=11∘32'
Also, minimum possible value of coefficient of friction
μ=tanθ=v2rg=0.2041⇒μ=0.2041
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples2videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples5videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
A cyclist speeding at 6m/s in a circle of 36 m diameter makes an angle 0 with the verticl . What is the value of 0 ? Also , deter - mine the minimum possible value of the coefficient of friction between the tyres and the road .
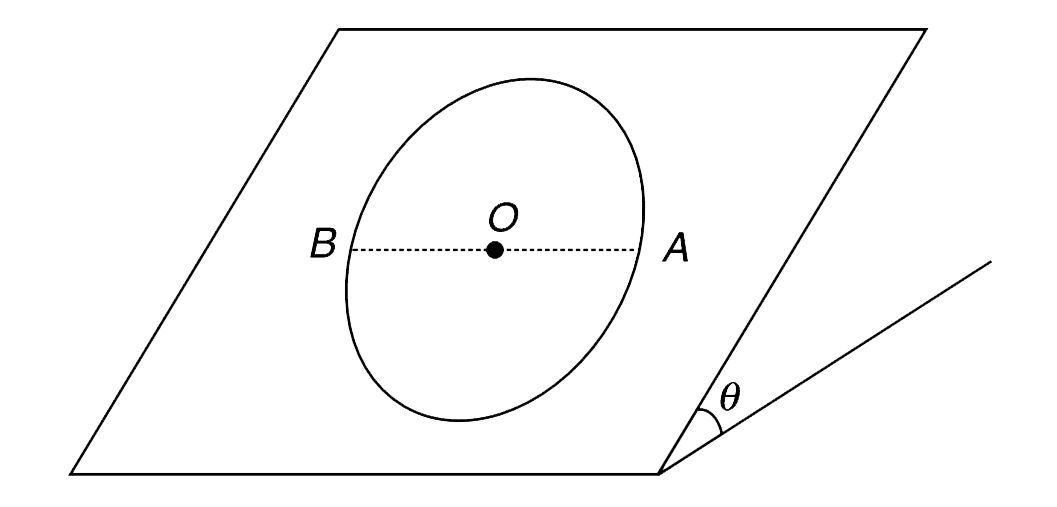
View SolutionA car is being driven on a tilted ground. The ground makes an angle θ with the horizontal. The driven drives on a circle of radius R. The coefficient of friction between the tires and the ground is μ.
(a) What is the largest speed for which the car will not slip at point A? Assume that rate of change of speed is zero.
(b) What is the largest constant speed with which the car can be driven on the circle without slipping?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid cylinder is rolling down on an inclined plane of angle θ. The minimum value of the coefficient of friction between the plane and the cylinder to allow pure rolling
A13tanθB23tanθC25tanθD45tanθ - Question 2 - Select One
What is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ
Av22μgB2v2μgCv2μgDnone of these - Question 3 - Select One
In the given system, a block of mass m is resting on a board which makes an angle θ with the horizontal. What should be the minimum value of θ, so that the block just starts moving downwards? The coefficient of friction between the surfaces of the board and the block is μ.
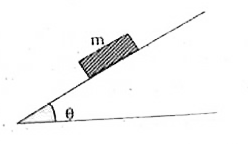 Atan−1(1/μ)Btan−1(μ)Csin−1μDnone
Atan−1(1/μ)Btan−1(μ)Csin−1μDnone
A motorcyclist is describing a circle of radius 25 m at a speed of 5 m/s . Find the inclination with the vertical and the coefficient of friction between the tyres and ground.
View SolutionWhat is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is μ.
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
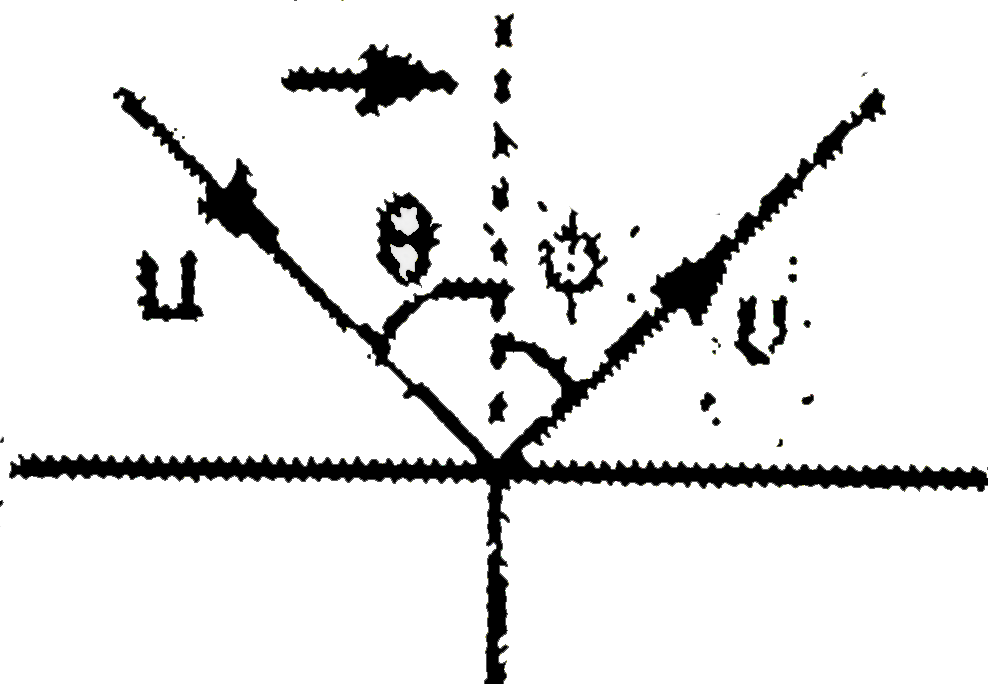 View Solution
View SolutionA circular road of radius 1000 m has banking angle 45∘. IF the coefficient of friction is between tyre and road is 0.5, then the maximum safe speed of a car having mass 2000 kg will be
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
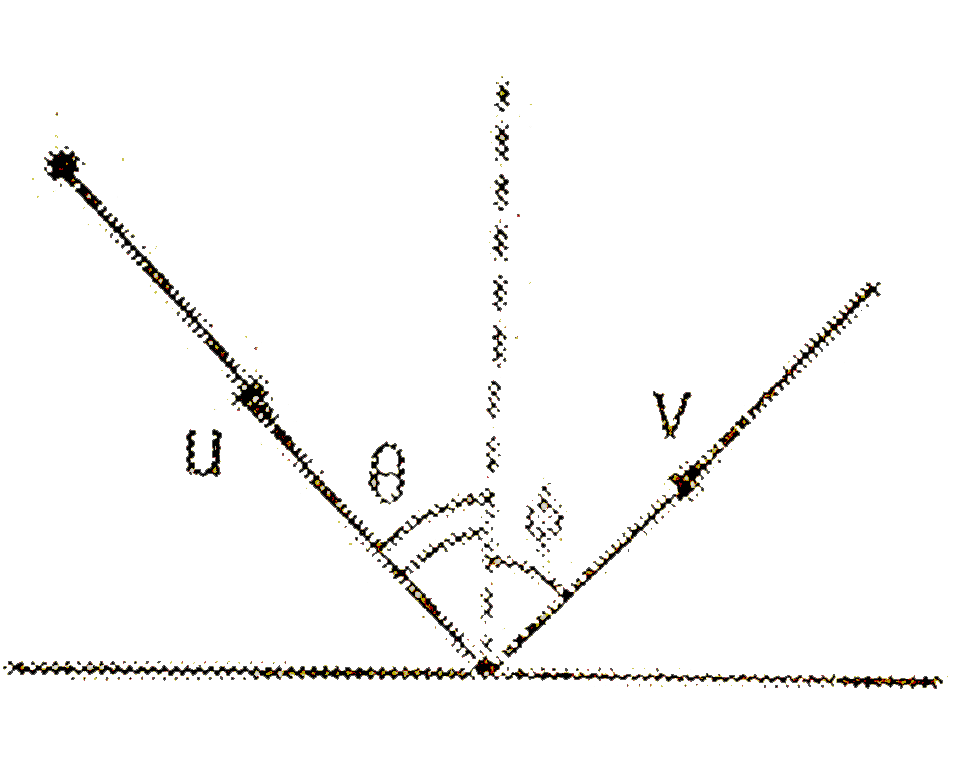 View Solution
View Solution

