A spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
The correct Answer is:C
To find the acceleration of a particle of mass m falling freely near the surface of a spherical planet with mass 2M and radius a, we can follow these steps:
Step 1: Identify the gravitational force acting on the particle
The gravitational force F acting on the particle of mass m due to the planet can be calculated using Newton's law of gravitation:
F=G⋅Mp⋅mr2
Where:
- G is the gravitational constant,
- Mp is the mass of the planet,
- r is the distance from the center of the planet to the particle (which is approximately the radius a of the planet when the particle is near the surface).
Step 2: Substitute the known values
Given that the mass of the planet Mp=2M and the radius r=a, we can substitute these values into the equation:
F=G⋅(2M)⋅ma2
Step 3: Calculate the gravitational field strength g
The gravitational field strength g at the surface of the planet is defined as the force per unit mass experienced by a small mass m:
g=Fm=G⋅(2M)a2
Step 4: Determine the acceleration of the particle
Since the particle is in free fall, its acceleration a is equal to the gravitational field strength g:
a=g=G⋅(2M)a2
Final Result
Thus, the acceleration of the particle falling freely near the surface of the planet is:
a=2GMa2
The gravitational force F acting on the particle of mass m due to the planet can be calculated using Newton's law of gravitation:
- G is the gravitational constant,
- Mp is the mass of the planet,
- r is the distance from the center of the planet to the particle (which is approximately the radius a of the planet when the particle is near the surface).
Given that the mass of the planet Mp=2M and the radius r=a, we can substitute these values into the equation:
The gravitational field strength g at the surface of the planet is defined as the force per unit mass experienced by a small mass m:
Since the particle is in free fall, its acceleration a is equal to the gravitational field strength g:
Thus, the acceleration of the particle falling freely near the surface of the planet is:
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.220videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Check Point 10.315videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective14videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE11videos
KINEMATICS
Similar Questions
A fixed spherical shell of inner radius R and outer radius 2R has mass M, A particle of mass m is held at rest at a distance 2R from the surface of the body. If the particle is released from that point, with what speed will it hit surface of the spherical body ?
View SolutionIf KE of the particle of mass m performing UCM in a circle of radius r is E. Find the acceleration of the particle
View Solution
Knowledge Check
- Question 1 - Select One
A spherical planet far out in space has a mass M0 and diameter D0. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
AGM0/D20B4mGm0/D20C4GM0/D20DGmM0/D20 - Question 2 - Select One
A spherical planet far out in space has a mass M0 and diameter D0. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity which is equal to
AGM0/D2B4mGM0/D20C4GM0/D20DGmM0/D20 - Question 3 - Select One
A spherical planet far out in space has a mass M0 and diameter D0. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
AGM0/D20B4mGM0/D20C4GM0/D20DGmM0/D20
A thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View Solution_S01_036_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass and radius 2R as shown. A small particle of mass m is relased from rest from a height h(<<R) above the shell. There is a hole in the shell.
Q. In what time will it enter the hole at AView Solution_E01_069_Q01.png)
A solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole inn the shell.
QIn what time will it enter the hole at AView SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.
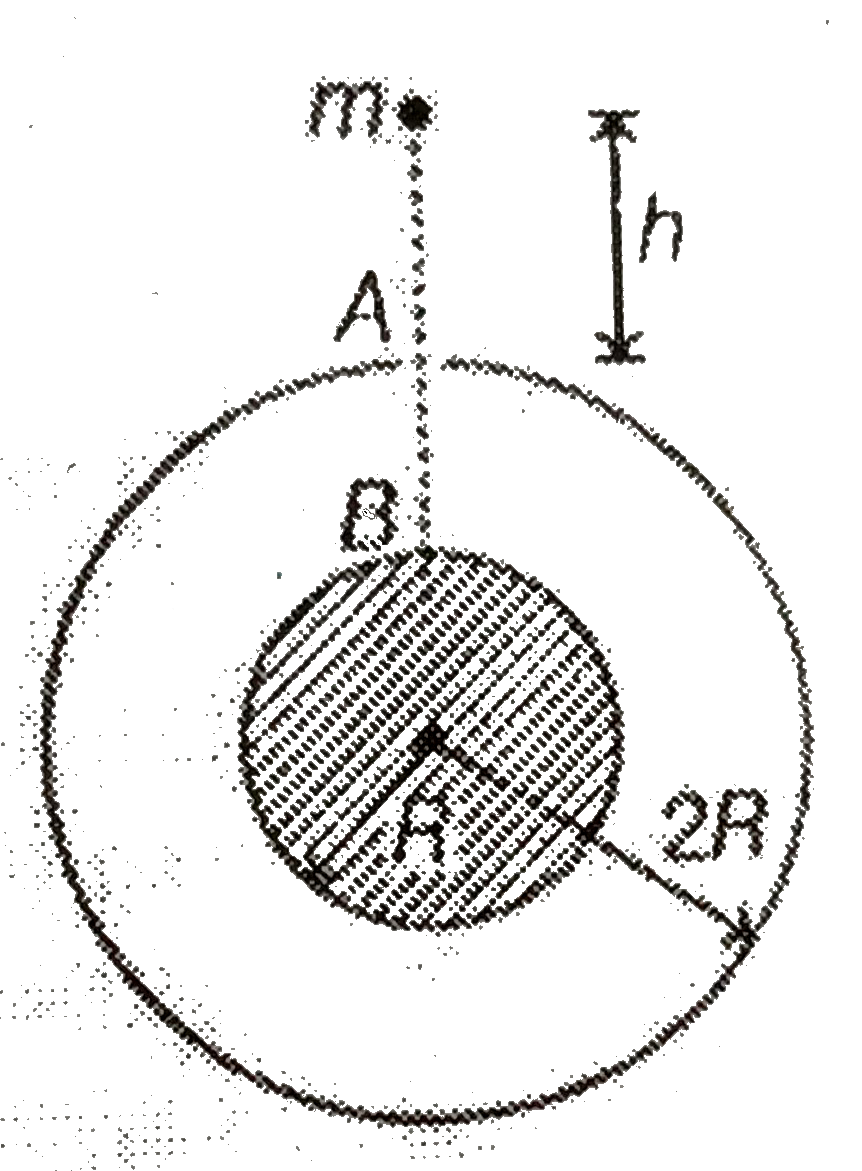
What speed will it collide at B?View SolutionA solid sphere of mass M and radius R is surrounded by a spherical shell of same mass M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is a hole in the shell.

What time will it take to move from A to B?View Solution

