Question

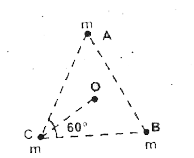
Three particles each of mass $m$ are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is

Options

A. zero
B. `(3GM)/(L^(2))`
C. `(9 GM)/(L^(2))`
D. `(12 GM)/(sqrt(3)L^(2))`

Answer

A

Explanation

To find the gravitational field at the center of an equilateral triangle formed by three particles each of mass $$m$$ located at the vertices, we can follow these steps:

1. Identify the Configuration:
We have three particles of mass \( m \) placed at the vertices of an equilateral triangle with side length \( L \). Let the vertices be labeled as A, B, and C.

2. Determine the Position of the Center:
The center of the equilateral triangle (centroid) is located at a distance of \( \frac{L}{\sqrt{3}} \) from each vertex.

3. Calculate the Gravitational Field Due to One Particle:
The gravitational field \( E \) due to a single particle at a distance \( r \) is given by the formula:
\( E = \frac{Gm}{r^2} \)
Here, \( r = \frac{L}{\sqrt{3}} \). Therefore, the gravitational field due to one particle at the center is:
\( E_A = \frac{Gm}{\left(\frac{L}{\sqrt{3}}\right)^2} = \frac{Gm \cdot 3}{L^2} = \frac{3Gm}{L^2} \)

4. Direction of the Gravitational Fields:
The gravitational field vectors \( E_A \), \( E_B \), and \( E_C \) due to particles at A, B, and C will point towards the respective particles. The angles between each pair of these vectors is \( 120^\circ \).

5. Vector Addition of Gravitational Fields:
Since the magnitudes of the gravitational fields are equal and the angles between them are \( 120^\circ \), we can use vector addition to find the resultant gravitational field at the center:
\( E_{\text{net}} = E_A + E_B + E_C \)
However, due to symmetry, the components of these vectors in any direction will cancel out. Therefore, the net gravitational field at the center will be:
\( E_{\text{net}} = 0 \)

Final Answer:
The gravitational field at the center of the triangle due to the three particles is \( \mathbf{0} \).

---