An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
1.3×102s
2.1×10−2s
1.6×10−10s
2.9×10−9s
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We have an electron falling in a uniform electric field. The distance it falls is given as s=1.5cm=0.015m, and the magnitude of the electric field is E=2×104N/C.
Step 2: Calculate the Force on the Electron
The force F acting on the electron can be calculated using the formula:
F=qE
where q is the charge of the electron, which is approximately q=−1.6×10−19C.
Substituting the values:
F=(−1.6×10−19C)(2×104N/C)=−3.2×10−15N
(Note: The negative sign indicates the direction of the force, but we will use the magnitude for calculations.)
Step 3: Calculate the Acceleration of the Electron
Using Newton's second law, F=ma, we can find the acceleration a:
a=Fm
where m is the mass of the electron, approximately m=9.1×10−31kg.
Substituting the values:
a=3.2×10−15N9.1×10−31kg≈3.51×1015m/s2
Step 4: Use the Equation of Motion
Since the electron starts from rest, we can use the second equation of motion:
s=ut+12at2
where u=0 (initial velocity), s=0.015m, and a is the acceleration we just calculated.
This simplifies to:
0.015=0+12(3.51×1015)t2
0.015=1.755×1015t2
Step 5: Solve for Time t
Rearranging the equation gives:
t2=0.0151.755×1015
Calculating t2:
t2≈8.54×10−18
Taking the square root to find t:
t≈√8.54×10−18≈2.92×10−9s
Final Answer
The time taken by the electron to fall a distance of 1.5 cm in the electric field is approximately t≈2.92ns.
---
We have an electron falling in a uniform electric field. The distance it falls is given as s=1.5cm=0.015m, and the magnitude of the electric field is E=2×104N/C.
The force F acting on the electron can be calculated using the formula:
F=qE
where q is the charge of the electron, which is approximately q=−1.6×10−19C.
F=(−1.6×10−19C)(2×104N/C)=−3.2×10−15N
(Note: The negative sign indicates the direction of the force, but we will use the magnitude for calculations.)
Using Newton's second law, F=ma, we can find the acceleration a:
a=Fm
where m is the mass of the electron, approximately m=9.1×10−31kg.
a=3.2×10−15N9.1×10−31kg≈3.51×1015m/s2
Since the electron starts from rest, we can use the second equation of motion:
s=ut+12at2
where u=0 (initial velocity), s=0.015m, and a is the acceleration we just calculated.
0.015=0+12(3.51×1015)t2
0.015=1.755×1015t2
Rearranging the equation gives:
t2=0.0151.755×1015
Calculating t2:
t2≈8.54×10−18
Taking the square root to find t:
t≈√8.54×10−18≈2.92×10−9s
The time taken by the electron to fall a distance of 1.5 cm in the electric field is approximately t≈2.92ns.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises20videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.520videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
Similar Questions
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
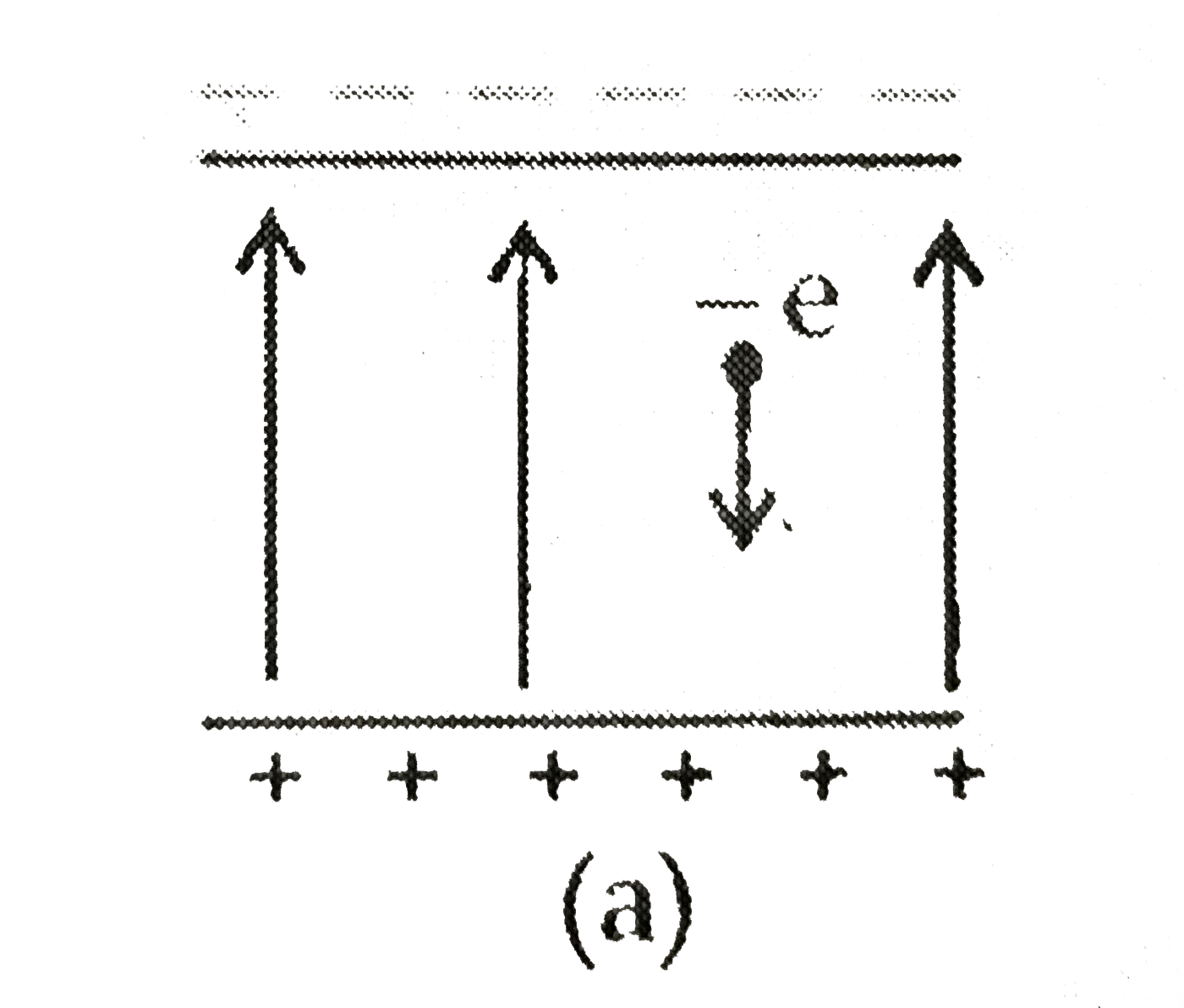
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest.
 View Solution
View SolutionAn electron falls through a distance 1.5 cm in a uniform electric field of magnitude 2.0×104NC−1 .Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed keeping its magnitude uncharged , calculate the time taken by a proton to fall through this distance starting from rest.
View Solution
Knowledge Check
- Question 1 - Select One
An electron initially at rest falls a distance of 2 cm in a uniform electric field of magnitude 3×104NC−1. The time taken by the electron to fall to this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.75×10−9s - Question 2 - Select One
An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
ASame in both casesBMore in the case of electronCMore in the case of protonDIndependent of charge
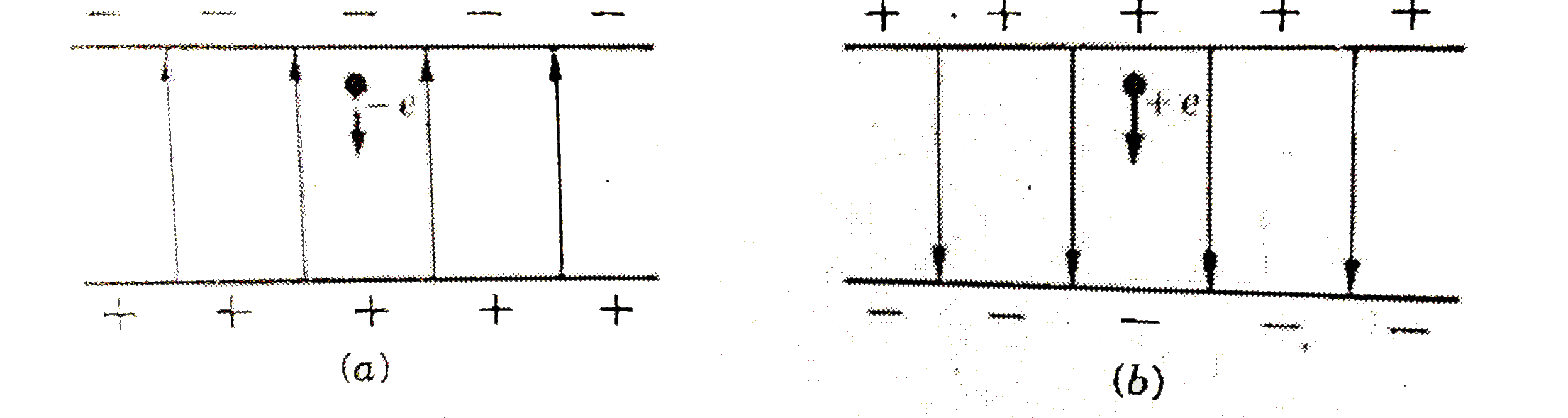
An electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
 View Solution
View SolutionAn electron falls through a distance of 1.5cm in a uniform electric field of value 2×104N/C, opposite to direction of fall. Compare the time of fall with 'free fall under gravity'.
View SolutionA proton falls dwon through a distance of 2 cm in a uniform electric field of magnitude 3.34×103NC−1. Determine (i) the acceleration of the electron (ii) the time taken by the proton to fall through the distance of 2 cm, and (iii) the direction of the electric field.
View SolutionAn electron is released from rest in a uniform electric field of magnitude 2.00×104N/C . (a) Calculate the acceleration of the electron. (Ignore gravitational) (b) How much time does the electron take to reach 1.00 % of the speed of light ?
View SolutionHow much deflection would the electron beam suffer when it travels a distance of 10 cm in a uniform electric field of 20 N/C . The initial velocity of electrons is 3×107 m/s directed perpendicular to the electric field .
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
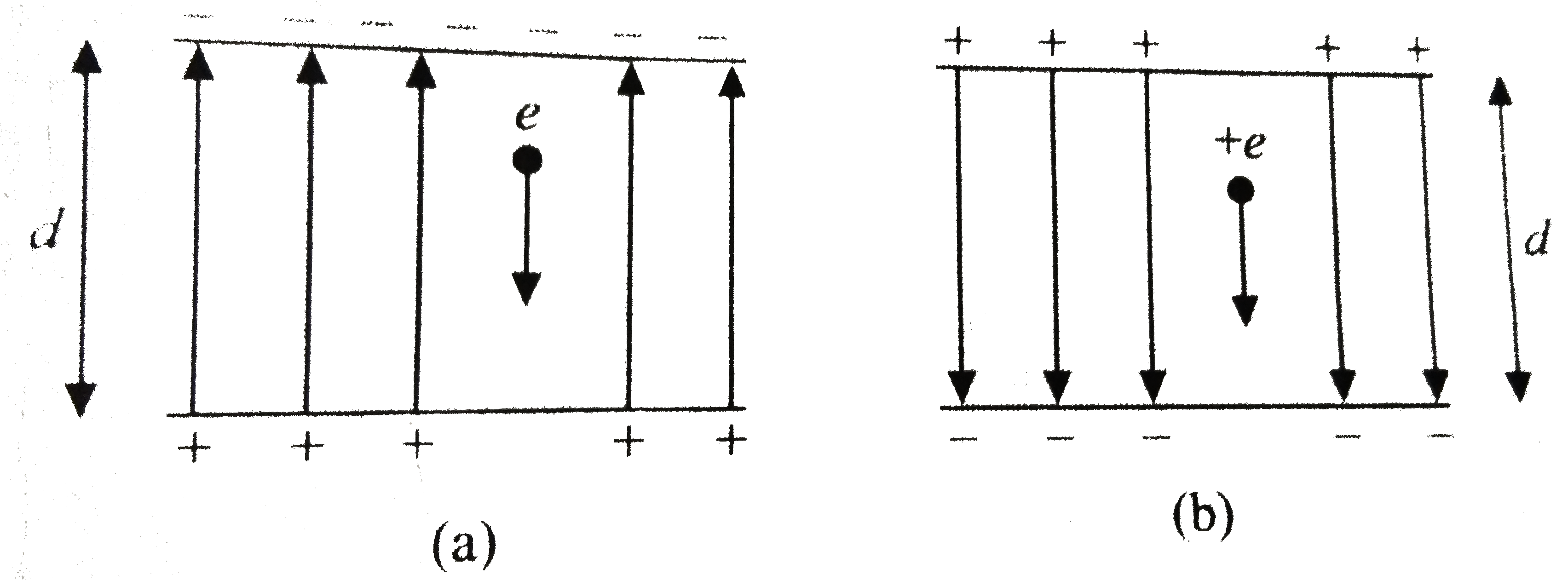 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.View Solution

