Two thin dielectric slabs of dielectric constants K1 and K2(K1<K2) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by





The correct Answer is:B
Step by step video, text & image solution for Two thin dielectric slabs of dielectric constants K_(1) and K_(2) (K_(1) lt K_(2)) are inserted between plates of a parallel plate capacitor, as shown in the figure. The variation of electric field E between the plates with distance d as measured from plate P is correctly shown by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises20videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
Similar Questions
Two dielectric slabs of dielectric constants K1andK2 are filled in between the two plates, each of area A, of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor.
 View Solution
View SolutionFind the capacitance between A and B if three dielectric slabs of dielectric constants K1areaA _(2)andthick≠ssd_(2))are∈sertedbetweentheplatesofaparal≤llate∩aci→rofplateareaA.(Giventˆthedistancebetweenthetwoplatesisd_(1)=d_(2)+d_(2).)
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreases - Question 2 - Select One
If the gap between the plates of a parallel plate capacitor is filled with medium of dielectric constant k=2 , then the field between them
AIncreases by a factor 2BIncreases by a factor √2CDecreased by a factor √2DDecreased by a factor 1/2 - Question 3 - Select One
Find the capacitance between A and B if two dielectric slabs (each of thickness d) of dielectric constants K1 and K2 and areas K1 and K2 and inserted between the plates of a parallel plate capacitor of plate area A.
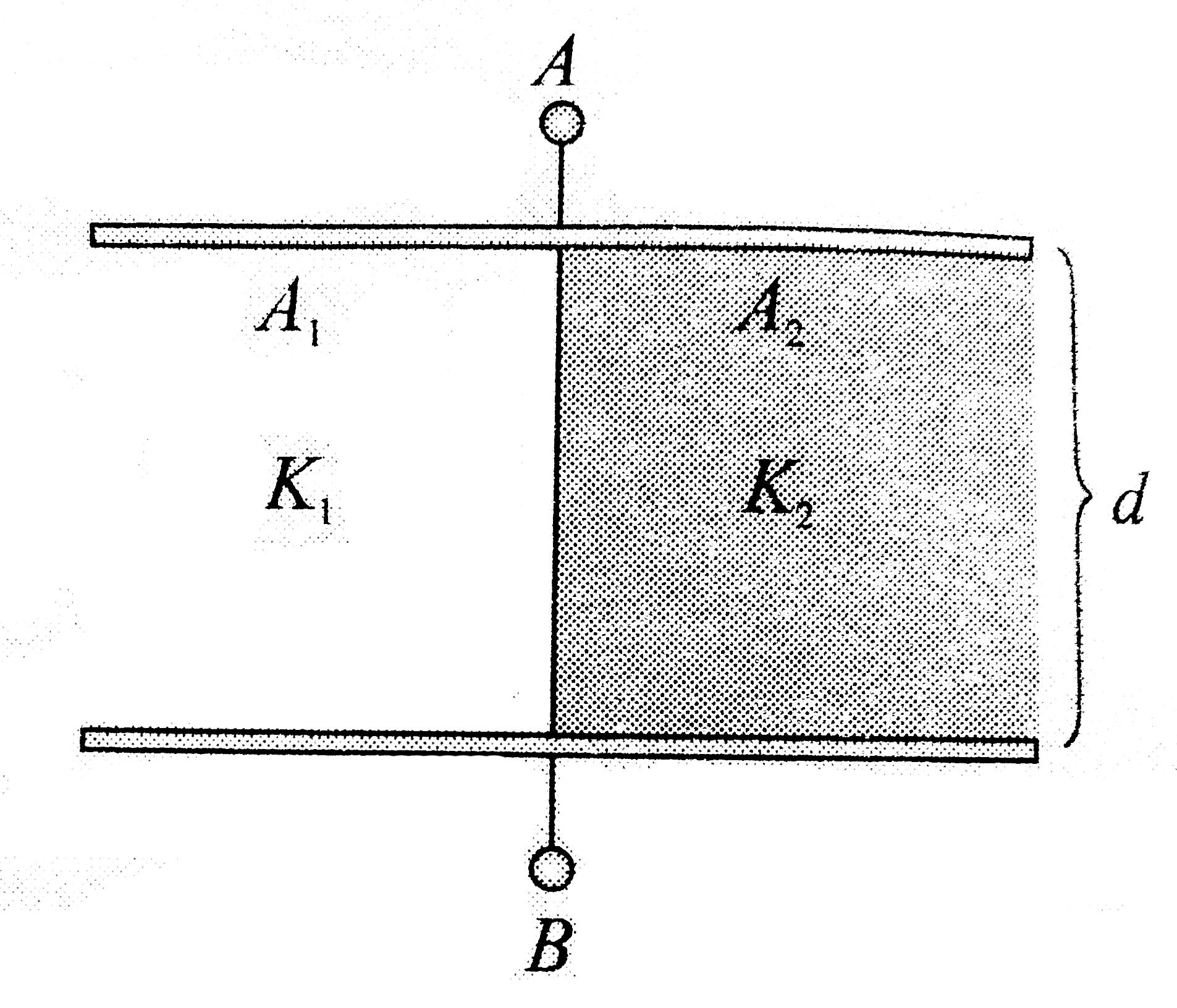 .ACequivalent=K1ε0A2d=ε0d(K1A1+K2A1)BCequivalent=ε0d(K2A1+K2A2)CCequivalent=K1ε0A2d=ε0d(K1A1+K2A2)DCequivalent=K1ε0A2d=ε0d(K1A1+K22A2)
.ACequivalent=K1ε0A2d=ε0d(K1A1+K2A1)BCequivalent=ε0d(K2A1+K2A2)CCequivalent=K1ε0A2d=ε0d(K1A1+K2A2)DCequivalent=K1ε0A2d=ε0d(K1A1+K22A2)
Two dielctric slabs of constant K1 and K2 have been filled in between the plates of a capacitor as shown below. What will be the capacitance of the capacitor ?
 View Solution
View SolutionIf a dielectric slab of thickness 5 mm and dielectric constant K=6 is introduced between the plates of a parallel plate air capacitor, with plate separation of 8 mm, then its capacitance is
View SolutionFind the capacitance between A and B if two dielectric alabs (each of area A) of dielectric constants K1 and K2 and thicknesses d1 and d2 are inserted between the plates of a parallel plate capacitor of plate area A.
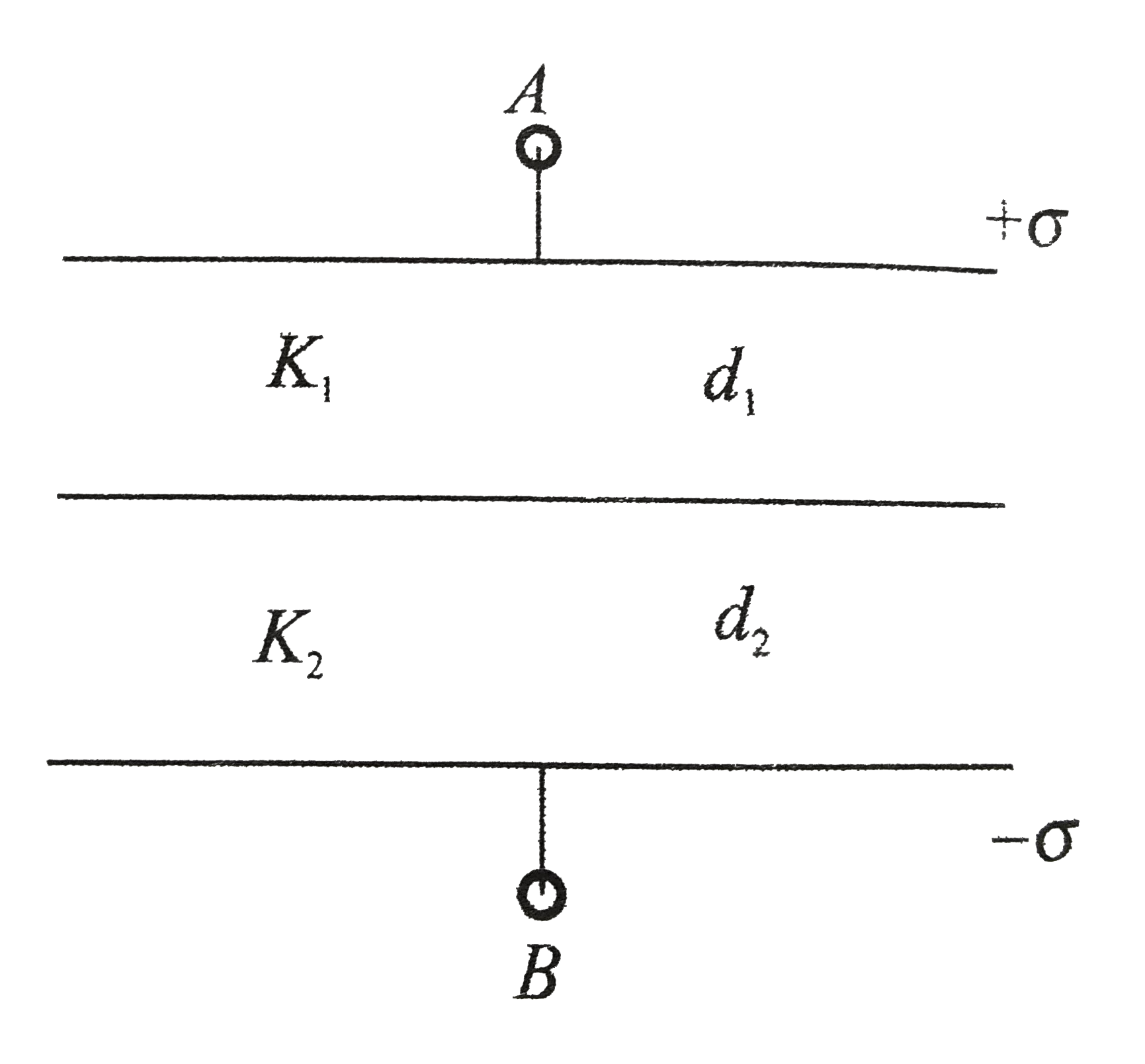 .View Solution
.View SolutionA parallel plate capacitor carries a harge Q. If a dielectric slab with dielectric constant K=2 is dipped between the plates, then
View SolutionTwo material having the dielectric constans K1 and K2 are filled between two parallel plates of a capacitor.
where area of each plate is A and the distance between the plates is d.
The capacitor of the capacitor is:
 View Solution
View Solution

