Assertion Maganetic field (B) and electric field (E) are present in a this region. Net force on a charged particle in this region is zero , if
E=B×v
Reason E/B has the dimensions of velocity.
The correct Answer is:b
To solve the problem, we need to analyze the assertion and the reason provided in the question step by step.
Step 1: Understanding the Assertion
The assertion states that the net force on a charged particle in a region with both magnetic field (B) and electric field (E) is zero if the condition E=B×v is satisfied.
Step 2: Force on a Charged Particle
The forces acting on a charged particle (with charge Q) in an electric field and a magnetic field can be expressed as:
- The electric force FE=Q⋅E
- The magnetic force FM=Q⋅(v×B)
Step 3: Setting the Net Force to Zero
For the net force to be zero, we can write:
Fnet=FE+FM=0
This implies:
Q⋅E+Q⋅(v×B)=0
Dividing through by Q (assuming Q≠0):
E+(v×B)=0
This can be rearranged to:
E=−(v×B)
This indicates that the electric field E is equal in magnitude but opposite in direction to the magnetic force (v×B).
Step 4: Analyzing the Reason
The reason states that EB has the dimensions of velocity. To analyze this, we can look at the dimensions of electric field E and magnetic field B:
- The dimension of electric field E is (E)=ML2T3A
- The dimension of magnetic field B is (B)=MLT2A
Calculating EB:
EB=ML2T3AMLT2A=LT
This is indeed the dimension of velocity.
Step 5: Conclusion
Both the assertion and the reason are true. However, the reason does not directly explain the assertion. The assertion is about the condition for the net force to be zero, while the reason discusses the dimensional analysis of the ratio of electric and magnetic fields.
Final Answer
- Assertion: True
- Reason: True
- Explanation: The reason does not explain the assertion.
The assertion states that the net force on a charged particle in a region with both magnetic field (B) and electric field (E) is zero if the condition E=B×v is satisfied.
The forces acting on a charged particle (with charge Q) in an electric field and a magnetic field can be expressed as:
- The electric force FE=Q⋅E
- The magnetic force FM=Q⋅(v×B)
For the net force to be zero, we can write:
Fnet=FE+FM=0
This implies:
Q⋅E+Q⋅(v×B)=0
Dividing through by Q (assuming Q≠0):
E+(v×B)=0
This can be rearranged to:
E=−(v×B)
This indicates that the electric field E is equal in magnitude but opposite in direction to the magnetic force (v×B).
The reason states that EB has the dimensions of velocity. To analyze this, we can look at the dimensions of electric field E and magnetic field B:
- The dimension of electric field E is (E)=ML2T3A
- The dimension of magnetic field B is (B)=MLT2A
EB=ML2T3AMLT2A=LT
This is indeed the dimension of velocity.
Both the assertion and the reason are true. However, the reason does not directly explain the assertion. The assertion is about the condition for the net force to be zero, while the reason discusses the dimensional analysis of the ratio of electric and magnetic fields.
- Assertion: True
- Reason: True
- Explanation: The reason does not explain the assertion.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following4videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together75videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
Similar Questions
Knowledge Check
- Question 1 - Select One
An electron enters a region where magnetic field (B) and electric field (E ) are mutually perpendicular, then
Ait will always move in the direction of BBit will always move in the direction of ECit always possess circular motionDit can go undeflected also - Question 2 - Select One
A charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
Aq(v×B)BqE+q(v×B)CqB+q(B×v)DqB+q(E×v) - Question 3 - Select One
A uniform magnetic field B and a uniform electric field E act in a common region. An electron is entering this region of space. The correct arrangement for it to escape undeviated is
A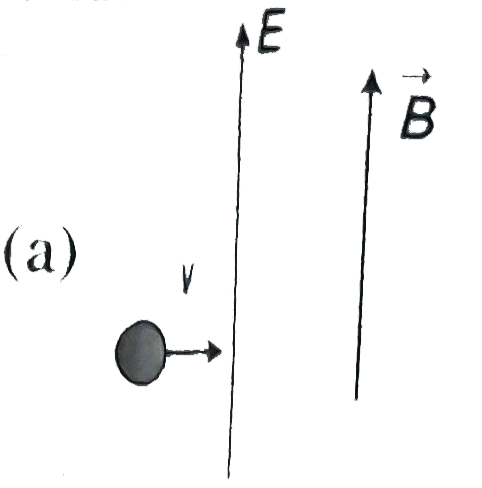 B
B C
C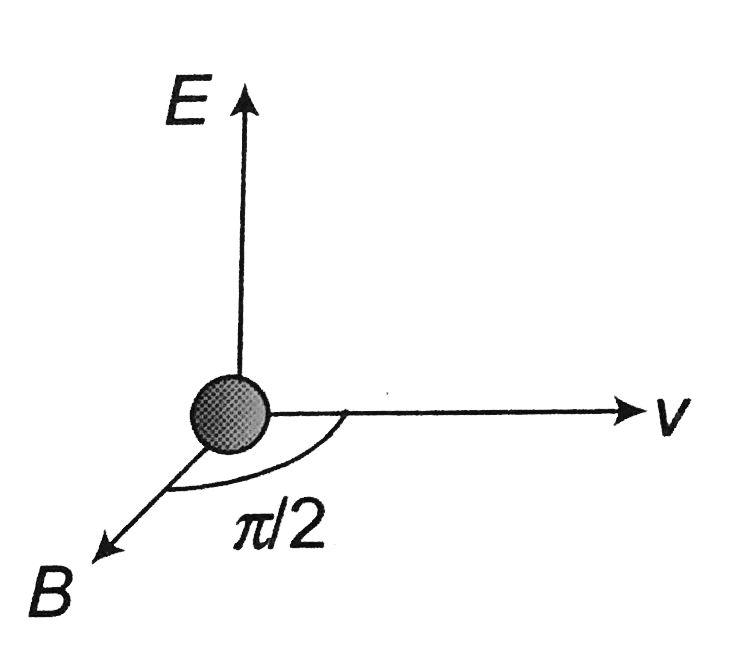 D
D
Assertion A beam of electron can pass undeflected through a region of E and B.
Reason Force on moving charged particle due to magnetic field may be zero in some cases.View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View SolutionAssertion: Electric field inside a current carrying wire is zero.
Reason: Net charge on the current carrying wire is non zero.View SolutionForce acting on a moving charged particle in a region of electric and magnetic fields is called
View SolutionIn a certain region of space electric field E and magnetic field B are perpendicular ot each other and an electron enters region perpendicular to the direction of B and E both and moves undeflected, then velocity of electron is
View Solution

