Assertion At the centre of a circular current carrying loop (I1), there is an infinitely long straight of the circle. Then magnetic force of attraction between two is zero.
Reason Magnetic field of I1 at centre is inwards, parallel to I2.
The correct Answer is:a
To solve the given question, we need to analyze both the assertion and the reason provided.
1. Understanding the Assertion:
The assertion states that at the center of a circular current-carrying loop (I₁), there is an infinitely long straight wire (I₂) along the axis of the circle. The claim is that the magnetic force of attraction between the two is zero.
2. Understanding the Reason:
The reason provided states that the magnetic field (B₁) produced by the circular loop at its center is directed inwards and is parallel to the current in the straight wire (I₂).
3. Magnetic Field at the Center of the Loop:
The magnetic field at the center of a circular loop carrying current (I₁) is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space and R is the radius of the loop. The direction of this magnetic field can be determined using the right-hand thumb rule, which indicates that it is directed into the plane of the loop.
4. Direction of Current in the Straight Wire:
If the current in the straight wire (I₂) is directed into the plane of the paper, then it is parallel to the magnetic field produced by the circular loop (B₁).
5. Force on the Straight Wire:
The force experienced by a current-carrying conductor in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
where θ is the angle between the direction of the current and the magnetic field. Since the magnetic field (B₁) and the current (I₂) are parallel, θ=0° and hence:
sin(0°)=0
Therefore, the force F becomes:
F=I⋅L⋅B⋅0=0
6. Conclusion:
Since the magnetic force of attraction between the circular loop and the straight wire is indeed zero, the assertion is correct. The reason provided also correctly explains why the force is zero.
Thus, both the assertion and reason are true, and the reason is the correct explanation for the assertion.
Final Answer:
Both the assertion and the reason are true, and the reason is the correct explanation for the assertion.
The assertion states that at the center of a circular current-carrying loop (I₁), there is an infinitely long straight wire (I₂) along the axis of the circle. The claim is that the magnetic force of attraction between the two is zero.
The reason provided states that the magnetic field (B₁) produced by the circular loop at its center is directed inwards and is parallel to the current in the straight wire (I₂).
The magnetic field at the center of a circular loop carrying current (I₁) is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space and R is the radius of the loop. The direction of this magnetic field can be determined using the right-hand thumb rule, which indicates that it is directed into the plane of the loop.
If the current in the straight wire (I₂) is directed into the plane of the paper, then it is parallel to the magnetic field produced by the circular loop (B₁).
The force experienced by a current-carrying conductor in a magnetic field is given by:
F=I⋅L⋅B⋅sin(θ)
where θ is the angle between the direction of the current and the magnetic field. Since the magnetic field (B₁) and the current (I₂) are parallel, θ=0° and hence:
sin(0°)=0
Therefore, the force F becomes:
F=I⋅L⋅B⋅0=0
Since the magnetic force of attraction between the circular loop and the straight wire is indeed zero, the assertion is correct. The reason provided also correctly explains why the force is zero.
Both the assertion and the reason are true, and the reason is the correct explanation for the assertion.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Match the following4videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together75videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE1videos
MAGNETICS
Similar Questions
Magnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
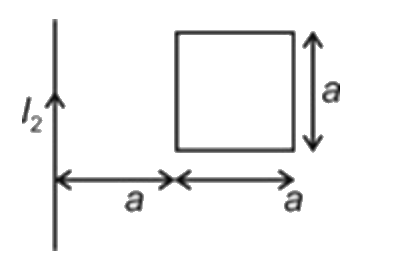
View SolutionIn the diagram shown, I1,I2 are the magnitudes of current in the squre loop and infinite long straight conductor respectively. If the net magnetic field at the centre of the loop is zero, then the relation between I1andI2 is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Assertion : A current I flows along the length of an infinitely long straight and thin walled pipe. Then the magnetic field at any point inside the pipe is zero.
Reason : ∮→B.d→l=μ0IAIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf the assertion and reason both are false. - Question 2 - Select One
A circular current carrying loop of radius R, carries a current l. The magnetic field at a point on the axis of coll is 1√8 times the value of magnetic field at the centre. Distance of point from centre is
AR√2BR√3CR√2DR - Question 3 - Select One
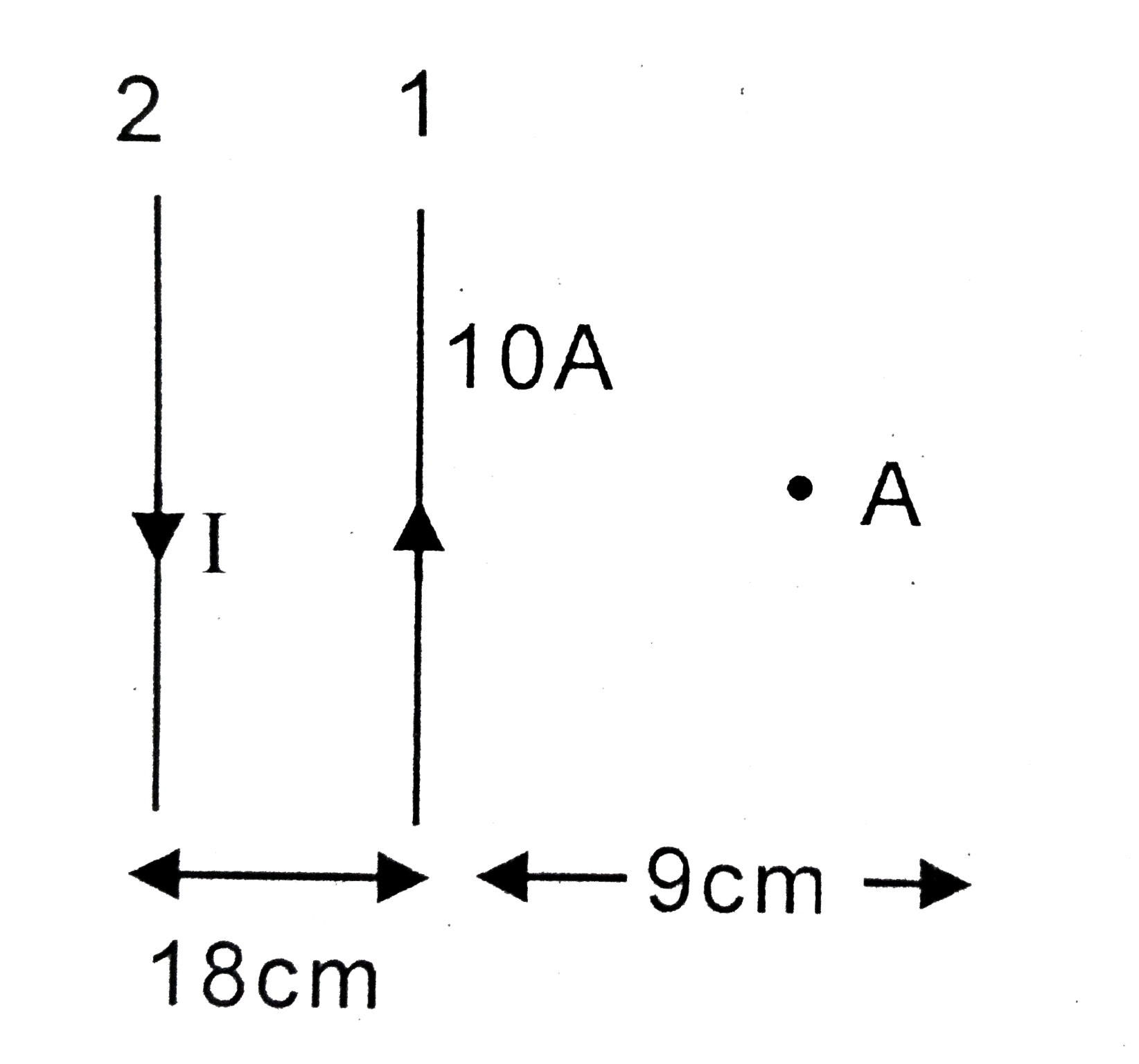
In figure two infinitely long current carrying wires are shown . If resultant magnetic field at point A is zero. Then determine current I1 .
 A50AB15AC30AD25A
A50AB15AC30AD25A
What is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionWhat is the direction of magnetic field at the centre of a current- carrying circular loop?
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionThe magnetic field at the centre of a current carrying circular loop is B. If the radius of the loop is doubled, keeping the current same, the magnetic field at the centre of the loop would be :
View SolutionAssertion Net torque in the current carrying loop placed in a uniform magnetic field (pointing inwards) is zero.

Reasonl Magnetic moment (M) is inwards.View Solution

