A battery of emf 12.0 V and internal resistance is to be charged by a battery charger which supplies 110 V d.c. How much resistance must be connected in series with the battery to limit the charging current to 5.0 A ? What will be the p.d. across the terminals of the battery during charging ?
To solve the problem, we need to determine the resistance that must be connected in series with the battery to limit the charging current to 5.0 A, and also find the potential difference across the terminals of the battery during charging.
1. Identify the Given Values:
- EMF of the battery (E) = 12.0 V
- Internal resistance of the battery (r) = 0.5 Ω
- Voltage of the charger (V) = 110 V
- Desired charging current (I) = 5.0 A
2. Apply Kirchhoff's Voltage Law (KVL):
According to KVL, the sum of the potential differences in a closed loop must equal zero. For our circuit:
V−E−I(r+R)=0
where R is the external resistance we need to find.
3. Rearrange the Equation:
Rearranging the equation gives:
V=E+I(r+R)
Substituting the known values:
110=12+5(0.5+R)
4. Simplify the Equation:
110=12+5(0.5)+5R
110=12+2.5+5R
110=14.5+5R
5. Solve for R:
110−14.5=5R
95.5=5R
R=95.55=19.1Ω
6. Calculate the Potential Difference Across the Battery:
The potential difference (V_b) across the terminals of the battery during charging can be calculated using:
Vb=E+I⋅r
Substituting the known values:
Vb=12+5⋅0.5
Vb=12+2.5=14.5V
Final Answers:
- The resistance R that must be connected in series is 19.1 Ω.
- The potential difference across the terminals of the battery during charging is 14.5 V.
- EMF of the battery (E) = 12.0 V
- Internal resistance of the battery (r) = 0.5 Ω
- Voltage of the charger (V) = 110 V
- Desired charging current (I) = 5.0 A
According to KVL, the sum of the potential differences in a closed loop must equal zero. For our circuit:
V−E−I(r+R)=0
where R is the external resistance we need to find.
Rearranging the equation gives:
V=E+I(r+R)
Substituting the known values:
110=12+5(0.5+R)
110=12+5(0.5)+5R
110=12+2.5+5R
110=14.5+5R
110−14.5=5R
95.5=5R
R=95.55=19.1Ω
The potential difference (V_b) across the terminals of the battery during charging can be calculated using:
Vb=E+I⋅r
Substituting the known values:
Vb=12+5⋅0.5
Vb=12+2.5=14.5V
- The resistance R that must be connected in series is 19.1 Ω.
- The potential difference across the terminals of the battery during charging is 14.5 V.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems From Competitive18videos
CURRENT ELECTRICITY
- BOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self101videos
CURRENT ELECTRICITY
- BOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B5videos
CHEMICAL EFFECT OF CURRENT
- BOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive61videos
ELECTRIC POTENTIAL AND ELECTRIC FLUX
Similar Questions
A storage battery of emf 12V and internal resistance of 1.5Ω is being charged by a 12 V supply. How much resistance is to be put in series for charging the battery safely, be maintaining a constant charging current of 6 A.
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View Solution
Knowledge Check
- Question 1 - Select One
A battery of emf 8 V with internal resistance 0.5Ω is being charged by a 120 V dc supply using a series resistance of 15.5Ω. The terminal voltage of the battery is
A20.5 VB15.5 VC11.5 VD2.5 V
A battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View SolutionA car battery of emf 12 V and internal resistance 0.1 Ω is being charged at a constant current of 5 A. The potential difference between the two terminals of the battery is ______.
View SolutionA battery of emf 10 V and internal resistance 3Ω is connected to a resistor. If the current in the circuit is 0.5 A, find (i) the resistance of the resistor, (ii) the terminal voltage of the battery.
View SolutionA series battery of six cells each of emf2V and internal resistance 0.5Ω is charged by a 100Vdc supply. What resistance should be used in the charging circuit in order to limit the charging current to 8A. Using this relation , obtain (a) the powwer supplied by the dc source, (b) the power dissipated as heat , and (c) the chemical energy stored in the battery in 15min.
View SolutionA storage battery of emf 8V and internal resistance is being charged by a 120 V D.C. supply using a series resistor of What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?
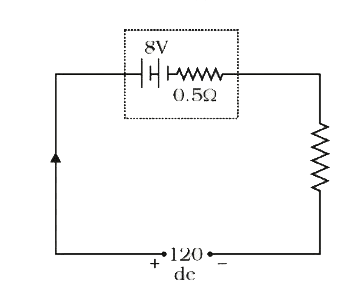 View Solution
View SolutionA battery of emf 2 V and internal resistance 0.5Ω is connected across a resistance of 9.5Ω. How many electrons pass through a cross-section of the resistance in 1 second ?
View Solution

