A fainter of the two stars of a binary system revolves around the brighter one in an orbit of semimajor axis with a period of 35 euars. Calculat the usm of the masses of the two stars of the binary system.
The correct Answer is:
Similar Questions
The angular separation betwenteh two components of a binary star system is of 3.5'' whereas the distance of the binary is 10.2 light years. If the two components of the binary revolve with a period of 45 years, calculate the sum of the masses of the two components in solar units.
View SolutionTwo stars of masses m1 and m2 form a binary system,revolving around each other in circular orbits of radii r1 and r2 respectively.Time period of revolution for this system is

View Solution
Knowledge Check
A system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
A2Gv3πTBv3TπGCv3T2πGD2Tv3πGA star of mass M (equal to the solar mass) with a planet (much smaller than the star) revolves around the star in a circular orbit. The velocity of the star with respect to the center of mass of the star-planet system is shown below :
 A0.004 A.U.B0.008 A.U.C0.004 A.U.D0.12 A.U.
A0.004 A.U.B0.008 A.U.C0.004 A.U.D0.12 A.U.The period of revolution of a planet around the sun in a circular orbit is same as that of period of similar planet revolving around a star of twice the raduis of first orbit and if M is the mass of the sun then the mass of star is
A2MB4MC8MD16M
The two components of Procyon have a separation of 4.55'' and period o 40.6 uears. If the distance of the binary is 11.3 light years, calculate the sum of the masses of the two stars in solar units. If the ratio of their masses is 3:1, find the mass of each star.
View SolutionConsider a binary star system consisting of two stars of masses M1 and M2 separated by a distance of 30AU with a period of revolution equal to 30 years. If one of the two stars is 5 times farther from the centre of mass than the other, show that the masses of the two stars are 5 and 25 times that of the sun.
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionA certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
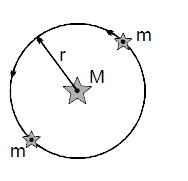
View SolutionThe small dense stars rotate about their common centre of mass as a binary system, each with a period of 1 year. One star has mass double than that of the other, while mass of the lighter star is one-third the mass of the Sun. The distance between the two stars is r and the distance of the earth from the Sun is R, find the relation between r and R.
View Solution
