Glycerine (refractive index 1.4) is poured into a large jar of radiys 0.2m to a depth of 0.1m. There is a small light source at the centre of the bottom of the jar. Find the area of the surface of glycerine through which the light passes.
To solve the problem of finding the area of the surface of glycerine through which light passes, we can follow these steps:
1. Identify the Given Data:
- Refractive index of glycerine, n=1.4
- Radius of the jar, R=0.2m
- Depth of glycerine, h=0.1m
2. Determine the Critical Angle:
The critical angle θc can be calculated using Snell's law. The formula for the critical angle when light is moving from a medium with a higher refractive index (glycerine) to a medium with a lower refractive index (air) is given by:
sinθc=n2n1
where n1=1.4 (glycerine) and n2=1.0 (air).
sinθc=1.01.4⟹θc=sin−1(11.4)
3. Calculate the Critical Angle:
Using a calculator,
θc≈sin−1(0.7143)≈45.57∘
4. Determine the Radius of the Circle of Light:
The light rays that can escape from the surface of glycerine will be those that hit the surface at an angle less than or equal to the critical angle. The relationship between the depth of glycerine and the radius r of the circle through which light passes is given by:
r=h⋅tan(θc)
Substituting the values,
r=0.1⋅tan(45.57∘)≈0.1⋅1.0≈0.1m
5. Calculate the Area of the Surface:
The area A of the circular surface through which light passes can be calculated using the formula for the area of a circle:
A=πr2
Substituting the value of r:
A=π(0.1)2=π⋅0.01≈0.0314m2
Final Answer:
The area of the surface of glycerine through which light passes is approximately 0.0314m2.
- Refractive index of glycerine, n=1.4
- Radius of the jar, R=0.2m
- Depth of glycerine, h=0.1m
The critical angle θc can be calculated using Snell's law. The formula for the critical angle when light is moving from a medium with a higher refractive index (glycerine) to a medium with a lower refractive index (air) is given by:
sinθc=n2n1
where n1=1.4 (glycerine) and n2=1.0 (air).
sinθc=1.01.4⟹θc=sin−1(11.4)
Using a calculator,
θc≈sin−1(0.7143)≈45.57∘
The light rays that can escape from the surface of glycerine will be those that hit the surface at an angle less than or equal to the critical angle. The relationship between the depth of glycerine and the radius r of the circle through which light passes is given by:
r=h⋅tan(θc)
Substituting the values,
r=0.1⋅tan(45.57∘)≈0.1⋅1.0≈0.1m
The area A of the circular surface through which light passes can be calculated using the formula for the area of a circle:
A=πr2
Substituting the value of r:
A=π(0.1)2=π⋅0.01≈0.0314m2
The area of the surface of glycerine through which light passes is approximately 0.0314m2.
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE A15videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - Problems For Self Practice109videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE J11videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - OPTICAL INSTRUMENTSEXERCISE - Problems for self practice35videos
OPTICAL INSTRUMENTS
- BOOK - SL ARORACHAPTER - SOLIDS AND SEMICONDUCTOR DEVICESEXERCISE - PROBLEM_TYPE9videos
SOLIDS AND SEMICONDUCTOR DEVICES
Similar Questions
A liquid of refractive index 1.5 is poured into a cyclindrical jar of radius 20 cm upto a height of 20 cm. A small bulb at the centre of bottom glowing. Find area of the liquid surface through which the light of the bulb passes into air.
View SolutionA point source of light is 80.0cm below the surface of a body of water. Find the diameter of the circle at the surface through which light emerges from the water.
View Solution
Knowledge Check
- Question 1 - Select One
Refractive index of water is 5/3. A light source is placed in water at a depth of 4m. Then what must be the minimum radius of disc placed on water surface so that the light of source can be stopped?
A3mB4mC5mD∞ - Question 2 - Select One
A horizontal cylinderical tank 6πm in diameter is half full of water. The space above the water is filled with a pressurized gas of unknown refractive index. A small laser can move along the curved bottom of the water and aims a light beam towards the centre of the water surface. When the laser has moved a distance s=1m or more (measured from curved face) from the lowest point in water, no light enters the gas. The refractive index of gas is (μwater=4/3)
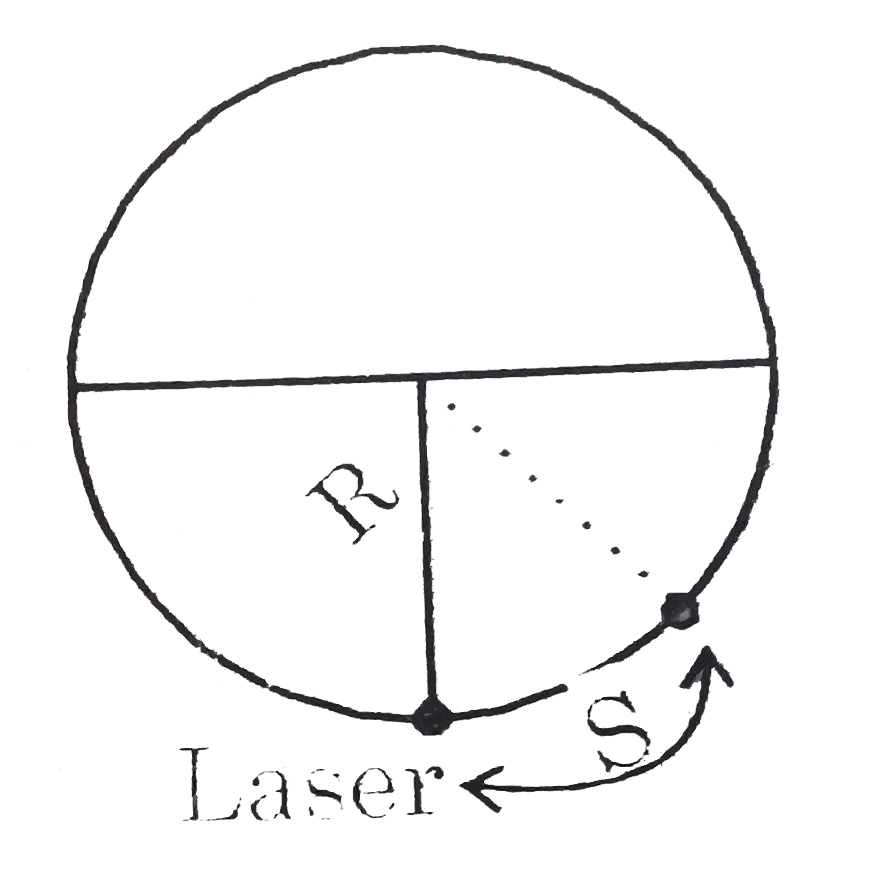 A4/√3B√5/2C2/√3D√3
A4/√3B√5/2C2/√3D√3 - Question 3 - Select One
A girl sees through a circular glass slab (refractive index 1.5) of thickness 20 mm and diameter 60 cm to the bottom of a swimming pool. Refractive index of water is 1.33. The bottom surface of the slab is in contact with the water surface.

The depth of swimming pool is 6m. The area of bottom of swimming pool that can be seen through the slab is approximately -A100m2B160m2C190m2D220m2
A horizontal cylindrical tank is half full of water ( refractive index =43) . The space above the water is filled with a light liquid of unknown refractive index (μ). A small laser source (s) can move along the curved bottom of the cylinder and aims a light beam towards the centre of the cylinder. The time needed by the laser beam to travel from the source to the rim of the cylinder depends on position (θ) of the source as shown in the graph. Find μ, it is given that sinθ0=56.
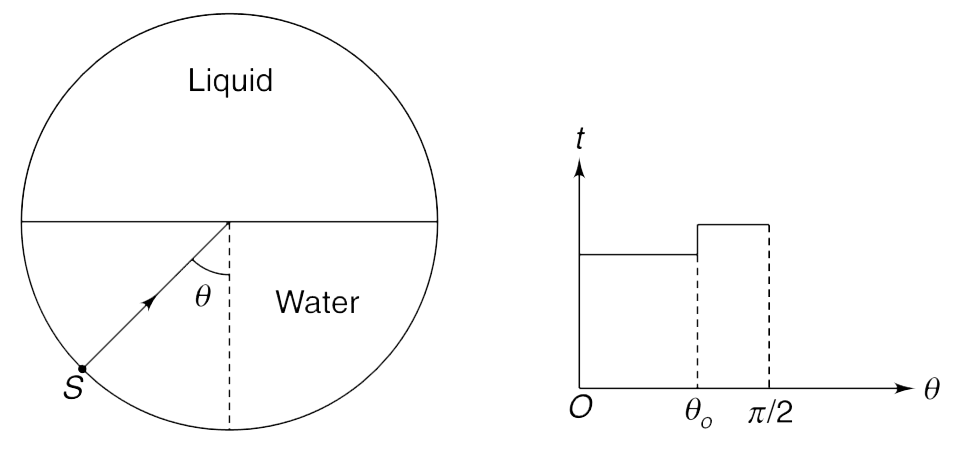 View Solution
View SolutionA point source of monochromatic light 'S' is kept at the centre of the bottom of a cylinder of radius 15.0cm. The cylinder contains water (refractive index 4//3) to a height of 7.0cm. Draw the ray diagram and calculate the area of water surface through which the light emerges in air.
View SolutionA point source of monochromatic light 'S' is kept at the centre of the bottom of a cylinder of radius 15.0cm. The cylinder contains water (refractive index 4//3) to a height of 7.0cm. Draw the ray diagram and calculate the area of water surface through which the light emerges in air.
View Solution(a) Define the term 'critical angle' for a pair of media
(b) A point source of monochromatic light S is kept at the centre of the bottom of a cylinder of radius 15.0 cm. The cylinder contains water (refractive index =43 to a height of 7.0 cm. Draw the ray diagram and calculate the area of water surface through which the light emerges in air.View SolutionA point light source is attached to the base of an empty trough. A transparent liquid of refractive index 1.35 is filled in the trough to a height of 50 cm. Calculate the total area on the surface of the liquid through which light will emerge.
View Solution

