A compound lens is made of two lenses having powers +15.5D and −5.5D. An object of 3cm height is placed at a distance of 30 cm from this compound lens. Find the size of the image.
The correct Answer is:−1.5cm
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the Power of the Compound Lens
The power of a lens is given in diopters (D). The total power P of a compound lens made of two lenses is the sum of their individual powers.
Given:
- Power of the first lens P1=+15.5D
- Power of the second lens P2=−5.5D
The total power P is calculated as:
P=P1+P2=15.5−5.5=10D
Step 2: Calculate the Focal Length of the Compound Lens
The focal length f of a lens in meters can be calculated from its power using the formula:
f=100P(in cm)
Substituting the total power:
f=10010=10cm
Step 3: Determine the Object Distance
The object distance u is given as 30 cm. Since the object is placed in front of the lens, we take it as negative in the lens formula:
u=−30cm
Step 4: Calculate the Magnification
The magnification m can be calculated using the formula:
m=ff+u
Substituting the values we have:
m=1010−30=10−20=−12
Step 5: Relate Magnification to Image Height
The magnification is also related to the heights of the object and the image:
m=h2h1
Where:
- h1 is the height of the object (3 cm)
- h2 is the height of the image
Rearranging the formula to find h2:
h2=m⋅h1=−12⋅3=−1.5cm
Conclusion
The size of the image is h2=−1.5cm. The negative sign indicates that the image is inverted.
---
The power of a lens is given in diopters (D). The total power P of a compound lens made of two lenses is the sum of their individual powers.
- Power of the first lens P1=+15.5D
- Power of the second lens P2=−5.5D
P=P1+P2=15.5−5.5=10D
The focal length f of a lens in meters can be calculated from its power using the formula:
f=100P(in cm)
Substituting the total power:
f=10010=10cm
The object distance u is given as 30 cm. Since the object is placed in front of the lens, we take it as negative in the lens formula:
u=−30cm
The magnification m can be calculated using the formula:
m=ff+u
Substituting the values we have:
m=1010−30=10−20=−12
The magnification is also related to the heights of the object and the image:
m=h2h1
Where:
- h1 is the height of the object (3 cm)
- h2 is the height of the image
h2=m⋅h1=−12⋅3=−1.5cm
The size of the image is h2=−1.5cm. The negative sign indicates that the image is inverted.
Topper's Solved these Questions
- RAY OPTICSBOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE F
10 Videos
- RAY OPTICSBOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE I
12 Videos
- RAY OPTICSBOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE A
15 Videos
- OPTICAL INSTRUMENTSBOOK - SL ARORACHAPTER - OPTICAL INSTRUMENTSEXERCISE - Problems for self practice
35 Videos
- SOLIDS AND SEMICONDUCTOR DEVICESBOOK - SL ARORACHAPTER - SOLIDS AND SEMICONDUCTOR DEVICESEXERCISE - PROBLEM_TYPE
9 Videos
Similar Questions
Knowledge Check
An object is placed at a distance of 10 cm from a convex lens of power 5 D. find the position of the image
A- 20 cmB30 cmC20 cmD- 30 cmAn object of height 2cm is held at a distance of 40cm in front of a concave lens of power −5D. Find the size of the image?
A2/3 cmB4/3 cmC7/8 cmD2/5 cm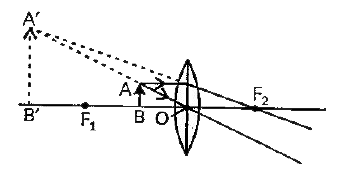
The above lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.A4 cmB6.67 mmC4 mmD3.33 mm
A convex lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.
View Solution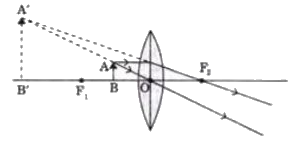
The above lens has a focal length of 10 cm. The object of height 2 mm is placed at a distance of 5 cm from the pole. Find the height of the image.
View SolutionA biconvex lens has equal radii of curvature of 20 cm for each face and is made of material of refractive index 1.5. An object of 6 cm height is placed at a distance of 10 cm from the lens. Find the position, nature and size of the image.
View SolutionThe focal length of convex lens is 20 cm. If an object of height 4 cm is placed at a distance of 30 cm from the lens, find:
The height of the image
View SolutionAn object of height 4 cm is placed at a distance of 15 cm in front of a concave lens of power, −10 dioptres. Find the size of the image.
View Solution