A ray of light is incident on the glass prism at an angle of 40∘. Find the angle of emergence, if the angle of prism is 60∘ and refractive index is 1.5.
The correct Answer is:58.5∘
To solve the problem, we will follow these steps:
Step 1: Understand the given data
- Angle of incidence (i) = 40°
- Angle of prism (A) = 60°
- Refractive index (μ) = 1.5
Step 2: Use Snell's Law to find the angle of refraction (r)
Using Snell's Law:
μ=sinisinr
We can rearrange this to find r:
sinr=siniμ
Substituting the values:
sinr=sin40°1.5
Step 3: Calculate the value of r
Now, we need to calculate sin40°:
sin40°≈0.6428
Thus,
sinr=0.64281.5≈0.4285
Now, we find r using the inverse sine function:
r=sin−1(0.4285)≈25.5°
Step 4: Find the angle of incidence for the second surface (i')
The angle of incidence on the second surface (i') can be found using:
i′=A−r=60°−25.5°=34.5°
Step 5: Use Snell's Law again to find the angle of emergence (r')
Now, we apply Snell's Law again at the second interface:
μ=sini′sinr′
Rearranging gives:
sinr′=μ⋅sini′
Substituting the values:
sinr′=1⋅sin34.5°
Calculating sin34.5°:
sin34.5°≈0.5660
Thus,
r′=sin−1(0.5660)≈34.5°
Step 6: Conclusion
The angle of emergence (r') is approximately 34.5°.
Summary of Steps
1. Identify given values.
2. Apply Snell's Law to find the angle of refraction (r).
3. Calculate the angle of incidence for the second surface (i').
4. Apply Snell's Law again to find the angle of emergence (r').
- Angle of incidence (i) = 40°
- Angle of prism (A) = 60°
- Refractive index (μ) = 1.5
Using Snell's Law:
μ=sinisinr
We can rearrange this to find r:
sinr=siniμ
Substituting the values:
sinr=sin40°1.5
Now, we need to calculate sin40°:
sin40°≈0.6428
Thus,
sinr=0.64281.5≈0.4285
Now, we find r using the inverse sine function:
r=sin−1(0.4285)≈25.5°
The angle of incidence on the second surface (i') can be found using:
i′=A−r=60°−25.5°=34.5°
Now, we apply Snell's Law again at the second interface:
μ=sini′sinr′
Rearranging gives:
sinr′=μ⋅sini′
Substituting the values:
sinr′=1⋅sin34.5°
Calculating sin34.5°:
sin34.5°≈0.5660
Thus,
r′=sin−1(0.5660)≈34.5°
The angle of emergence (r') is approximately 34.5°.
1. Identify given values.
2. Apply Snell's Law to find the angle of refraction (r).
3. Calculate the angle of incidence for the second surface (i').
4. Apply Snell's Law again to find the angle of emergence (r').
Topper's Solved these Questions
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE F10videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE I12videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - RAY OPTICSEXERCISE - TYPE A15videos
RAY OPTICS
- BOOK - SL ARORACHAPTER - OPTICAL INSTRUMENTSEXERCISE - Problems for self practice35videos
OPTICAL INSTRUMENTS
- BOOK - SL ARORACHAPTER - SOLIDS AND SEMICONDUCTOR DEVICESEXERCISE - PROBLEM_TYPE9videos
SOLIDS AND SEMICONDUCTOR DEVICES
Similar Questions
A ray of light is incident on a 60∘ glass prism at an angle of 60∘. Find the
the angle of emergence
the angle of deviation, given the refractive index of glass = 1.5.View SolutionA ray of light falls on a glass prism at a angle of incidence of 30∘. Find the direction of the emergent ray if the angle of the prism is 60∘ and refractive index is 1.50
View Solution
Knowledge Check
- Question 1 - Select One
A monochromatic ray of light strikes one face of a prism at an angle of 60∘ and the angle of refraction is 30∘ . The refracting angle of the prism is 60∘ . What is the angle of emergence ?
A30∘B45∘C50∘D60∘ - Question 2 - Select One
A ray of light is incident on one of the faces of the angle prism with an angle 40∘ with the surface. The angle of the prism is 60∘. The emergent ray is deviated through an angle 38∘. The angle of emergence is
A38∘B48∘C52∘D58∘ - Question 3 - Select One
A ray of light incident on a prism of angle 60∘, does not emerge out. Refractive index of material of prism may be
A1.50B2.30C1.80D1.20
A ray of light is incident on one face of a prism (μ=1.5) at an angle of 60∘. The refracting angle of the prism is also 60∘. Find the angle of emergence and the angle of deviation. Is there any other angle of incidence, which will produce the same deviation?
View SolutionA ray of light is incident on one face of a prism (m=√3) at an angle of 60∘. The refracting angle of the prism is also 60∘. Find the angle of emergence .
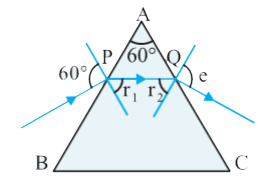 View Solution
View SolutionA ray of light is incident at an angle of 60∘ on the face of a prism with an angle of 60∘. Then the refractive index of the material of the prism is (the prism is in minimum deviation position)
View SolutionA ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
View SolutionA ray of light is incident at 65∘ on one face of a prism of angle of 30∘ and the emergent ray makes 35∘ with the incident ray. The refractive index of the prism is:
View Solution

