The distance time graph of a particle at time t makes angle 45∘ with respect to time axis. After 1s, if makes angle 60∘ with respect to time axis. What is the acceleration of the particle?
(√3−1) unit
(√3+1) unit
√3 unit
1 unit
To solve the problem step-by-step, we will analyze the distance-time graph and calculate the acceleration of the particle based on the angles given.
Step 1: Understand the relationship between slope and velocity
The slope of a distance-time graph represents the velocity of the particle. The angle made with the time axis can be used to calculate the slope using the tangent function.
Step 2: Calculate the initial velocity (v1)
At time t=0 seconds, the angle is 45∘.
Using the tangent function:
tan(45∘)=1
This means the slope (velocity) at this point is:
v1=1m/s
Step 3: Calculate the velocity after 1 second (v2)
After 1 second, the angle is 60∘.
Using the tangent function again:
tan(60∘)=√3
This means the slope (velocity) at this point is:
v2=√3m/s
Step 4: Calculate the change in velocity
The change in velocity (Δv) is given by:
Δv=v2−v1=√3−1m/s
Step 5: Calculate the time interval
The time interval (Δt) over which this change occurs is:
Δt=1s(from t=0 to t=1 second)
Step 6: Calculate the acceleration (a)
Acceleration is defined as the change in velocity divided by the time interval:
a=ΔvΔt=√3−11=√3−1m/s2
Final Answer
The acceleration of the particle is:
a=√3−1m/s2
---
The slope of a distance-time graph represents the velocity of the particle. The angle made with the time axis can be used to calculate the slope using the tangent function.
At time t=0 seconds, the angle is 45∘.
Using the tangent function:
tan(45∘)=1
This means the slope (velocity) at this point is:
v1=1m/s
After 1 second, the angle is 60∘.
Using the tangent function again:
tan(60∘)=√3
This means the slope (velocity) at this point is:
v2=√3m/s
The change in velocity (Δv) is given by:
Δv=v2−v1=√3−1m/s
The time interval (Δt) over which this change occurs is:
Δt=1s(from t=0 to t=1 second)
Acceleration is defined as the change in velocity divided by the time interval:
a=ΔvΔt=√3−11=√3−1m/s2
The acceleration of the particle is:
a=√3−1m/s2
Topper's Solved these Questions
Similar Questions
The distance time graph of a body is a st. line making an angle of 30∘ with time axis. What is speed ?
View Solution(a) The distance time graph of a body makes an angle of 30∘ with time axis, Figure. What is its velocity ?
(b) If the same makes an angle of 30∘ with distance axis, Figure, what is the velocity of the body ?
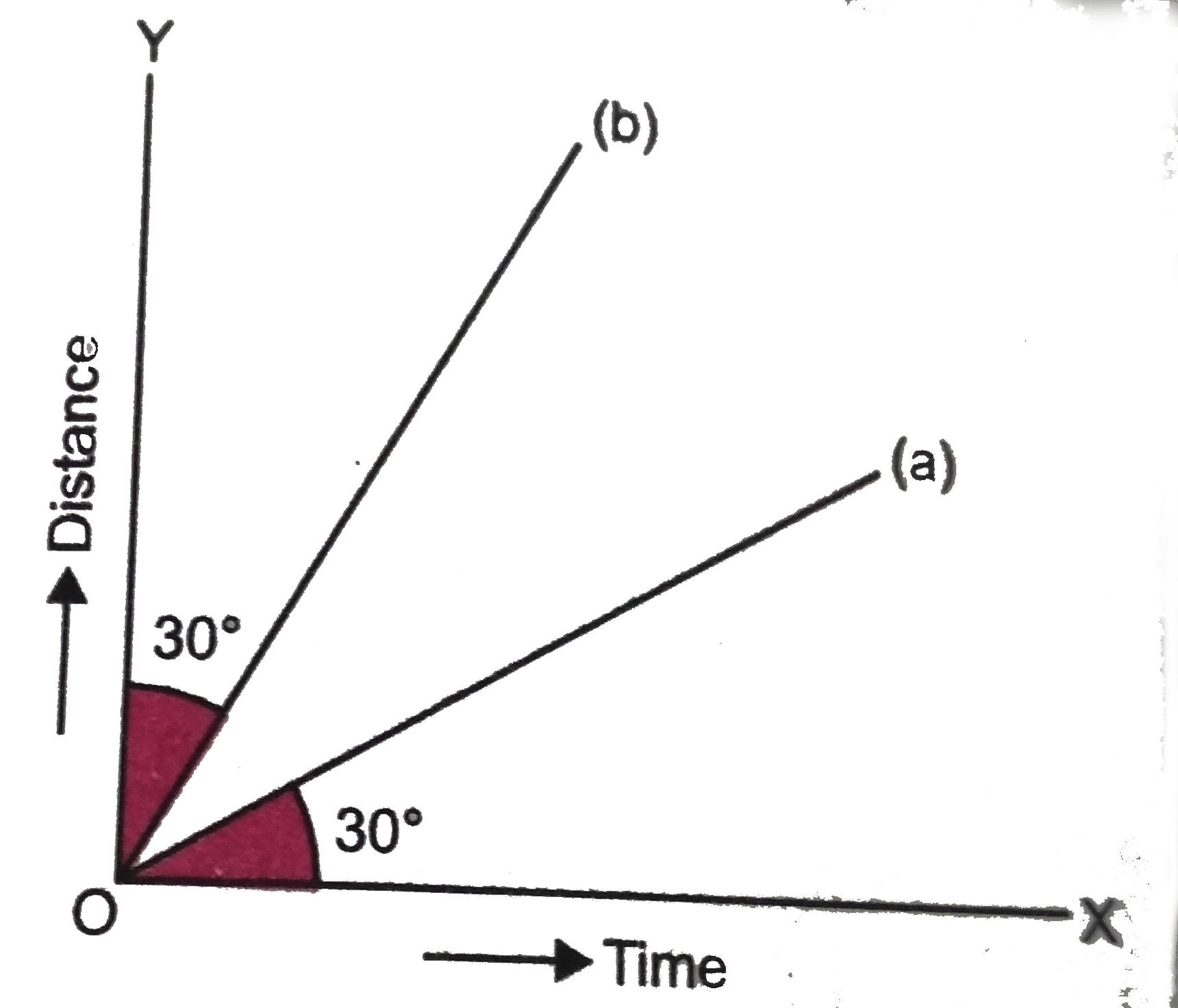
View Solution
Knowledge Check
Displacement-time curve of a particle moving along a straight line is shown. Tangents at A and B makes angle 45∘ and 135∘ with positive x-axis respectively. The average acceleration of the particle during t=1,t=2 seconds is
 A−2m/s2B1m/s2C−1m/s2Dzero
A−2m/s2B1m/s2C−1m/s2DzeroIn displacement time graph, two straight lines make angles 60∘and30∘ with time axis. The ratio of mangnitudes of the velocities represented by them is
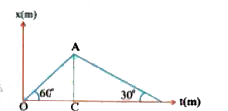 A1:2B1:3C2:1D3:1
A1:2B1:3C2:1D3:1
The v-t graphs of two objects make angles of 30∘ and 60∘ with the time-axis. Find the ratio of their accelerations.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View SolutionThe displacement time graph for two particles AandB are straight lines inclined at 30∘ with time axis and at 30∘ to displacement axis respectively. Calcualte ratio of velocities of the two particles.
View SolutionIf the displacement-time of a particle is parallel to (b) displacement axis (b) the time axis,
what will be the velcity of the particle ?
View Solution(a) The distance time graph of a body is parallel to the time axis. What does it indicate ?
(b) The distance time graph of a body coincide with time axis. What does it indicate ?
View SolutionThe v-t graphs of two objects make angles of 30∘ and 60∘ with the time-axis. Find the ratio of their accelerations.
View Solution
