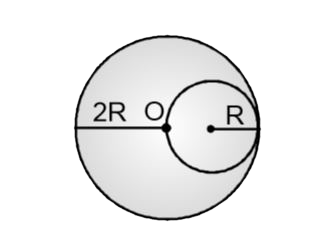
Mass of bigger disc having radius 2R is M. A disc of radius R is cut from bigger disc. Moment of intertia of disc about an axis passing through periphery and perpendicular to plane is

A

$\frac{27 M R^{2}}{8}$

B

$\frac{29 M R^{2}}{8}$

C

3.5 MR

D

2 M $R^{2}$

Video Solution

Text Solution

Verified by Experts

b) Surface density of motional disc is
$σ = (\frac{M}{π {(2 R)}^{2}} = \frac{M}{4 π R^{2}}$
Mass of cutting portion is
$m_{1} = σ \times π R^{2} = \frac{M}{4}$
$I = I_{1} - I_{2}$
Where,
$I_{1}$ = Moment of inertia of disc about given axis without cutting portion
$I_{2}$ = Moment of inertia due to cutting portion
$I = \frac{M {(2 R)}^{2}}{2} + M {(2 R)}^{2} - [\frac{m_{1} R^{2}}{2} + m_{1} {(2 R)}^{2}]$
$6 M R^{2} - \frac{9 M R^{2}}{8} = \frac{39 M R^{2}}{8}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A $(M R^{2}$
B $\frac{3}{2} M R [^(2)$
C $\frac{M R^{2}}{2}$
D $\frac{5}{4} M R^{2}$
Question 2 - Select One
From a disc of mass 2kg and radius 4m a small disc of radius 1 m with center O' is extracted . The new moment of inertia,about an axis passing through O perpendicular to plane of disc is

A $16 k g m^{2}$
B $12 k g m^{2}$
C $\frac{255}{16} k g m^{2}$
D $\frac{247}{16} k g m^{2}$
Question 3 - Select One
The radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is
A2 m
B2 cm
C1 m
D0.2 m

BITSAT GUIDE-ROTATIONAL MOTION-BITSAT Archives

Home
Ask Doubt
Profile