In (Q. 24.) if at t = 0, y = 2.5 mm, the equation of standing wave is
The correct Answer is:C
The equation of standing wave on a string fixed both ends is
Here, 2a = 5 mm
Topper's Solved these Questions
Similar Questions
Figure shows the standing waves pattern in a string at t = 0. Find out the equation of the standing wave where the amplitude of antinode is 2A.
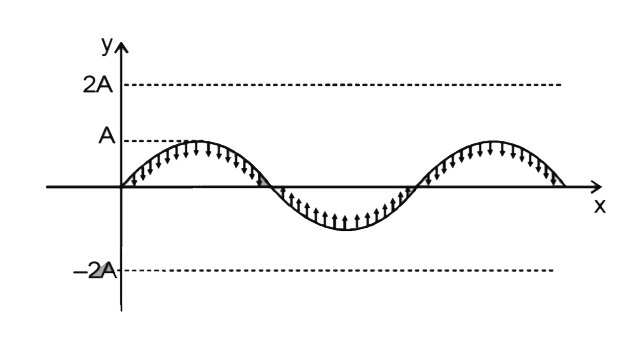
View SolutionTwo sine waves of same frequency and amplitude, travel on a stretched string in opposite directions. Speed of each wave is 10 cm/s. These two waves superimpose to form a standing wave pattern on the string. The maximum amplitude in the standing wave pattern is 0.5 mm. The figure shows the snapshot of the string at t = 0.Write the equation of the two travelling waves.

View Solution
Knowledge Check
A string of length l along x-axis is fixed at both ends and is vibrating in second harmonic. If at t=0, y=2.5mm for incident wave, the equation of standing wave is (T is tension and μ is linear density)
A(2.5mm)sin(2πlx)cos(2π√(Tμl2)t)B(5mm)sin(πlx)cos2πtC(5mm)sin(2πlx)cos(2π√(Tμl2)t)D(5mm)cos(2πlx)cos(2π√(Tμl2)t)In an organ pipe ( may be closed or open of 99cm length standing wave is setup , whose equation is given by longitudinal displacement ξ=(0.1mm)cos(2π)0.8(y+1cm)cos2π(400)t
where y is measured from the top of the tube in metres and t in second. Here 1cm is th end correction.

The air column is vibrating inAPex=(125πN/m2)sin(2π)0.8(y+1cm)cos2π(400t)BPex=(125πN/m2)cos(2π)0.8(y+1cm)sin2π(400t)CPex=(225πN/m2)sin(2π)0.8(y+1cm)cos2π(200t)DPex=(225πN/m2)cos(2π)0.8(y+1cm)sin2π(200t)In an organ pipe (may be closed or open ) of 99cm length standing wave is set up , whose equation is given by longitudinal displacement.

ξ=(0.1mm)cos(2π)0.8(y+1cm)cos(400)twhere y is measured from the top of the tube in metres and tinseconds . Here 1cm is the end correction.
Equation of the standing wave in terms of excess pressure is ( take bulk modulus =5×105N/m2))APex=(125πN/m2)sin(2π)0.8(y+1cm)cos(400t)BPex=(125πN/m2)cos(2π)0.8(y+1cm)sin(400t)CPex=(225πN/m2)sin(2π)0.8(y+1cm)cos(200t)DPex=(225πN/m2)cos(2π)0.8(y+1cm)sin(200t)
At time t=0,y(x) equation of a wave pulse is
y=102+(x−4)2
and at t=2s, y(x) equation of the same wave pulse is
y=102+(x+4)2
Here, y is in mm and x in metres. Find the wave velocity.
View SolutionWrite the equation of a wave identical to the wave represented by the equation y=5sinπ(4.0t−0.02x), but moving in opposite direction. Write the equation of stationary wave produced by the combination of these two waves. Determine the distance between two nearest nodes. All distances in the equations are in mm.
View SolutionA standing wave is represented by y=2Asinkxcosωt. If one of the component waves is y1=Asin(ωt−kx), what is the equation of the second component wave?
View SolutionIn an organ pipe ( may be closed or open of 99cm length standing wave is setup , whose equation is given by longitudinal displacement ξ=(0.1mm)cos(2π)0.8(y+1cm)cos2π(400)t
where y is measured from the top of the tube in metres and t in second. Here 1cm is th end correction.

Equation of the standing wave in terms of excess pressure is -
(Bulk modulus of air B=5×105N/m2)
View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0. The equation fo the refelcted wave is :
View Solution
