Two sine waves of same frequency and amplitude, travel on a stretched string in opposite directions. Speed of each wave is 10 cm/s. These two waves superimpose to form a standing wave pattern on the string. The maximum amplitude in the standing wave pattern is 0.5 mm. The figure shows the snapshot of the string at t = 0.Write the equation of the two travelling waves.

The correct Answer is:y1=0.25sin(π4x+5π2t+3π4);
y2=0.25sin(π4x−5π2t+3π4)
Step by step video, text & image solution for Two sine waves of same frequency and amplitude, travel on a stretched string in opposite directions. Speed of each wave is 10 cm/s. These two waves superimpose to form a standing wave pattern on the string. The maximum amplitude in the standing wave pattern is 0.5 mm. The figure shows the snapshot of the string at t = 0.Write the equation of the two travelling waves. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Can two waves of the same frequency and amplitude travelling in the same direction give rise to a stationary wave after superposition ?
View SolutionFigure shows the standing waves pattern in a string at t = 0. Find out the equation of the standing wave where the amplitude of antinode is 2A.

View Solution
Knowledge Check
Two waves of equal frequency f and velocity v travel in opposite directions along the same path. The waves have amplitudes A and 3A . Then:
Athe amplitude of the resulting wave varies with position between maxima of amplitude 4A and minima of zero amplitude.Bthe distance between a maxima and adjacent minima of amplitudes is v/2fCmaximum amplitude is 4A and minimum amplitude is 2ADThe position of a maxima or minima of amplitude does not change with timeIf two waves of same frequency and same amplitude superimpose and produce third wave of same amplitude, then waves differ in phase by –
Aπ/3B2π/3Cπ/2DπA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0. The equation fo the refelcted wave is :
Ay'=0.5Asin(kx+ωt+θ)By'=−0.5Asin(kx+ωt+θ)Cy'=−0.5Asin(ωt−kx−θ)Dy'=0.5Asin(kx+ωt−θ)
The standing wave pattern shown in the tube has a wave speed of 5.0ms−1. What is the frequency of the standing wave [ in Hz approx.] ?

View SolutionIf two wave of the same frequency differ in amplitude and are propagated in opposite directions through a medium , will they produce standing waves ? Is energy transported ? Are there any nodes ?
View SolutionTwo waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
View SolutionFigure shows two wave opulses at t=0 travelling on a string i opposite directions with the same wave speed 50cms−1. Sketch the shape of the string at t=4ms, 6ms, 8ms and 12 ms.
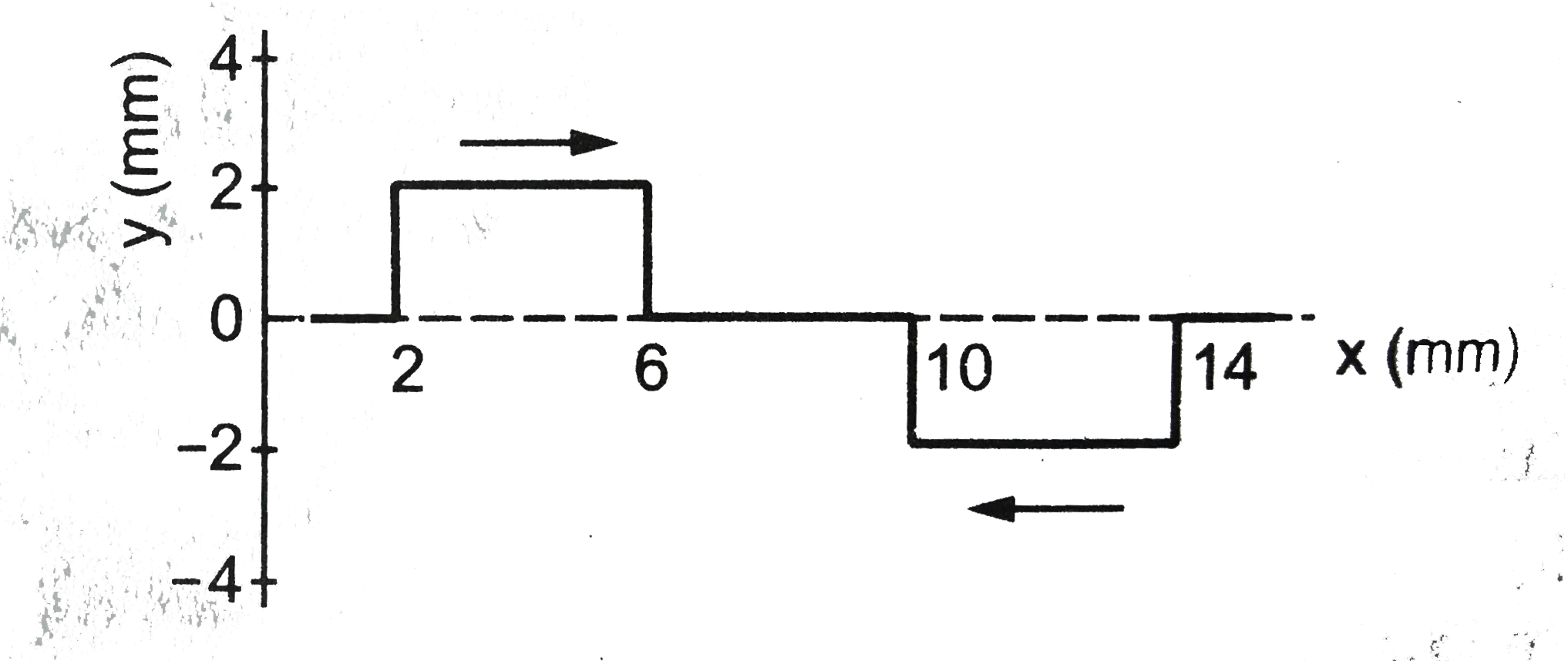 .
.
View SolutionShows a snapshot of a sinusoidal travelling wave taken at t=0.3s. The wavelength is 7.5 cm and amplitude is 2 cm. if the crest P was at x=0 at t=0, write the equation of travelling wave.
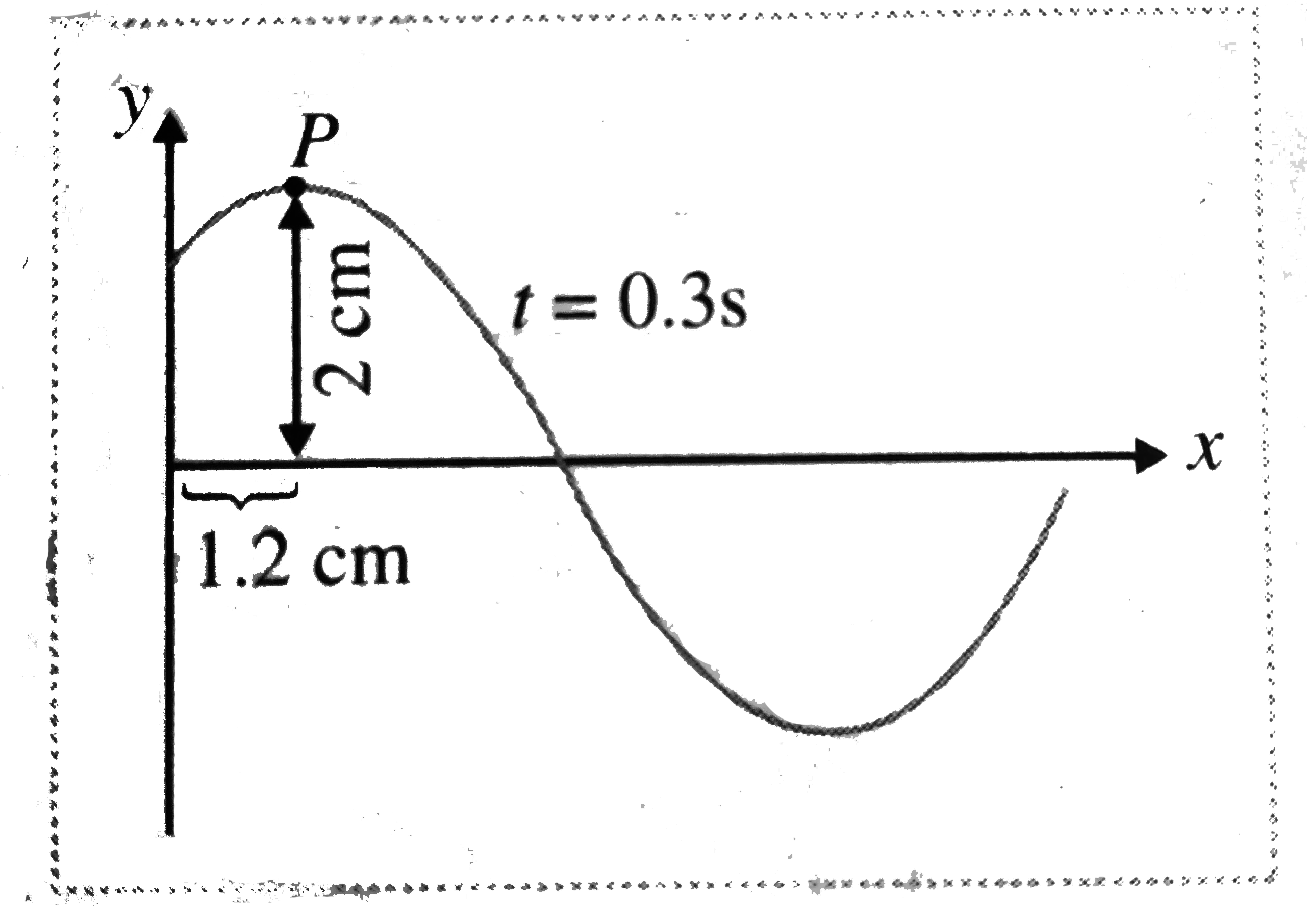
View Solution
