In a circle of radius R a square is inscribed, then a circle is inscribed in the square, a new square in the circle and so on for n times. If the ratio of the limit of the sum of areas of all the circles to the limit of the sum of areas of all the squares as n→∞ is k, then find the value of 4kπ.
Step by step video & image solution for In a circle of radius R a square is inscribed, then a circle is inscribed in the square, a new square in the circle and so on for n times. If the ratio of the limit of the sum of areas of all the circles to the limit of the sum of areas of all the squares as n->oo is k, then find the value of (4k)/pi. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A circle is inscribed ina n equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is
View SolutionA circle is inscribed in an equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is______
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
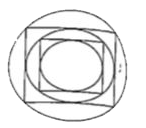
What is the sum of areas of all the squares shown in the figure ?
View SolutionA square is inscribed in a circle then another circle is inscribed in the square . Another square is then inscribed in the circle. Finally a circle is inscirbed in the innermost square . Thus there are 3 circles and 2 squares as shown in the figure . The radius of the outer - most circle is R .
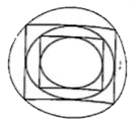
What is the ratio of sum of circumference of all the circles to the sum of perimeters of all the squares ?
View SolutionIf a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
View SolutionIf a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionA semi-circle and a circle with same radius inscribe a square of greatest possible area. What is the ratio of area of square inscribed by semicircle to that by circle?
View SolutionA square is inscribed in a circle of radius R, a circle is inscribed in this square then a square in this circle and so on n times. Find the limit of the sum of areas of all the squares as n→∞.
View Solution