One slit of a double slit experiment is covered by a thin glass plate of refractive index 1.4, and the other by a thin glass plate of the refractive index 1.7. The point on the screen where the central maximum fall before the glass plate was inserted, is now occupied by what had been the fifth bright fringe was seen before. Assume the plate have the same thickness t and wavelength of light 480 nm. Then find the value of t in .
The correct Answer is:C
Step by step video, text & image solution for One slit of a double slit experiment is covered by a thin glass plate of refractive index 1.4, and the other by a thin glass plate of the refractive index 1.7. The point on the screen where the central maximum fall before the glass plate was inserted, is now occupied by what had been the fifth bright fringe was seen before. Assume the plate have the same thickness t and wavelength of light 480 nm. Then find the value of t in mum. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
One slit of a double slits experiment is covered by a thin glass plate of refractive index1.4and the other by a thin glass plate of refractive index1.7 .The point on the screen ,where central bright fringe was formed before the introduction of the glass sheets,is now occupied by the 15thbright fringe.Assuming that both the glass plates have same thickness and wavelength of light used in 4800Å ,find the their thickness.
View SolutionIn a double-slit experiment, fringes are produced using light of wavelength 4800A∘. One slit is covered by a thin plate of glass of refractive index 1.4 and the other slit by another plate of glass of double thickness and of refractive index 1.7. On doing so, the central bright fringe shifts to a position originally occupied by the fifth bright fringe from the centre. find the thickness of the glass plates.
View Solution
Knowledge Check
- Question 1 - Select One
In a young 's double slit experiment, a glass plate of refractive index 1.5 and thickness 5×10−4 cm is kept in the path of one of the light rays. Then
AThere will be no shift in the interference patternBThe fringe width will increasesCThe fringe width will decreasesDThe optical path of the ray will increases by 2.5×10−4cm - Question 2 - Select One
A ray of unpolarised light is incident on a glass plate of refractive index 1.54 at polarising angle, then angle of refraction is :
A33∘B44∘C57∘D90∘ - Question 3 - Select One
If a glass plate refractive index is 1.732 is to be used as a polariser, what would be the angle of refraction?
A30∘B60∘C45∘D35∘
A thin glass plate of thickness t and refractive index μ is between screen &one of the slits in young's experiment.if the intensity at the center of the screen is I ,was the intenstity at the same point prior to the introduction of the sheet.
(b) One slit of a young's experiment is covered by a glass plate (μ1=1.4) and the other by another glass plate (μ2=1.7) of the same thickness. The point of central maxima of the screen,before the plates were introduced is now occupied by the third bright fringe.Find the thicknes of the thickness of the plates.the wavelength of light used in 4000Å.View SolutionLight reflected from the surface of glass plate of refractive index 1.57 is linearly polarised. Calculate the angle of refraction in glass.
View SolutionA ray of light is incident on the surface of a glass plate of refractive index 1.6 at polarzing angle. Calculate the angles of reflection and refraction.
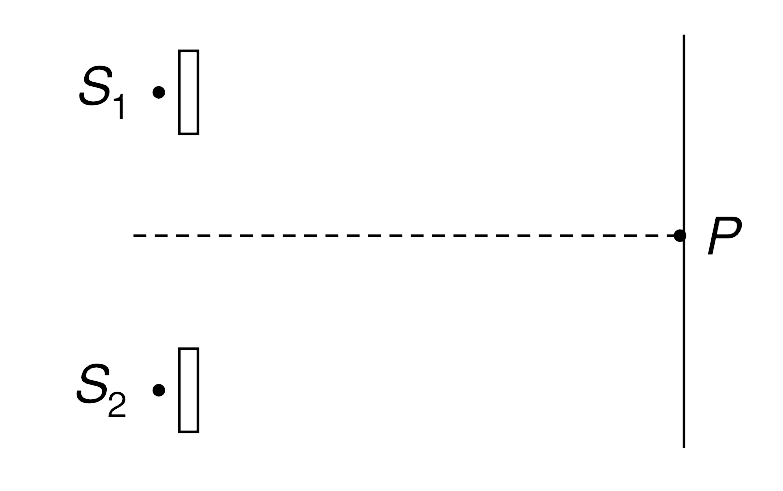
View SolutionIn Young’s double slit experiment, the upper slit is covered by a thin glass plate of refractive index 1.4 while the lower slit is covered by another glass plate having same thickness as the first one but having refractive index 1.7.
Interference pattern is observed using light of wavelength5400∘A. It is found that the point P on the screen where the central maximum fell before the glass plates were inserted, now has 34 the original intensity. It is also observed that what used to be 5th maximum earlier, lies below the point P while the6th minimum lies above P. Calculate the thick- ness of glass plates. Absorption of light by glass plate may be neglected.
 View Solution
View SolutionA thin glass plate of refractive index 1.5 is introduced in the path of one of the interfering beam. As a result, the central bright fringe moves to a position previously occupied by the fifth bright fringe. If the wavelength of beam is 6.2×10−5cm, calculate the thickness of glass plate.
View Solution

