A block starts moving up a fixed inclined plane of inclination 60∘C with a velocityof 20ms−1 and stops after 2s. The approximate value of the coefficient of friction is [g=10ms−2]
3
3.3
0.27
0.33
The correct Answer is:C
To solve the problem step by step, we will analyze the forces acting on the block moving up the inclined plane and use kinematics to find the coefficient of friction.
Step 1: Identify the forces acting on the block
The forces acting on the block moving up the inclined plane are:
- The gravitational force (weight) acting downward, mg.
- The normal force N acting perpendicular to the inclined plane.
- The frictional force Fk acting opposite to the direction of motion (down the incline).
Step 2: Resolve the gravitational force
The gravitational force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
Given that θ=60∘:
- sin60∘=√32
- cos60∘=12
Thus, the components are:
- mgsin60∘=mg⋅√32
- mgcos60∘=mg⋅12
Step 3: Write the equation of motion
Since the block is moving up the incline and then stops, the net force acting on it can be expressed as:
Fnet=−mgsin60∘−Fk
Where Fk=μN and N=mgcos60∘.
Substituting for N:
Fk=μ(mgcos60∘)=μ(mg⋅12)
Step 4: Set up the equation
The net force can also be expressed in terms of mass and acceleration:
Fnet=ma
Thus, we have:
−mgsin60∘−μ(mg⋅12)=ma
Since a is negative (retardation), we can express it as:
a=−g(12√3+μ2)
Step 5: Use kinematics to find acceleration
Using the kinematic equation:
v=u+at
Where:
- Final velocity v=0 (the block stops)
- Initial velocity u=20m/s
- Time t=2s
Substituting the values:
0=20+(−g(12√3+μ2))⋅2
Step 6: Solve for μ
Substituting g=10m/s2:
0=20−10(12√3+μ2)⋅2
0=20−10(√3+μ)
10(√3+μ)=20
√3+μ=2
μ=2−√3
Step 7: Calculate the approximate value of μ
Using the approximate value √3≈1.732:
μ≈2−1.732=0.268
Thus, the approximate value of the coefficient of friction μ is approximately 0.268.
The forces acting on the block moving up the inclined plane are:
- The gravitational force (weight) acting downward, mg.
- The normal force N acting perpendicular to the inclined plane.
- The frictional force Fk acting opposite to the direction of motion (down the incline).
The gravitational force can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- sin60∘=√32
- cos60∘=12
- mgsin60∘=mg⋅√32
- mgcos60∘=mg⋅12
Since the block is moving up the incline and then stops, the net force acting on it can be expressed as:
Fnet=−mgsin60∘−Fk
Where Fk=μN and N=mgcos60∘.
Fk=μ(mgcos60∘)=μ(mg⋅12)
The net force can also be expressed in terms of mass and acceleration:
Fnet=ma
Thus, we have:
−mgsin60∘−μ(mg⋅12)=ma
a=−g(12√3+μ2)
Using the kinematic equation:
v=u+at
Where:
- Final velocity v=0 (the block stops)
- Initial velocity u=20m/s
- Time t=2s
0=20+(−g(12√3+μ2))⋅2
Substituting g=10m/s2:
0=20−10(12√3+μ2)⋅2
0=20−10(√3+μ)
10(√3+μ)=20
√3+μ=2
μ=2−√3
Using the approximate value √3≈1.732:
μ≈2−1.732=0.268
Topper's Solved these Questions
Similar Questions
A block starts moving up an inclined plane of inclination 30∘ with an initial velocity of v0 . It comes back to its initial position with velocity v02 . The value of the coefficient of kinetic friction between the block and the inclined plane is close to I1000 , The nearest integer to I is ____________ .
View SolutionIf a block moving up an inclined plane at 30∘ with a velocity of 5 m/s, stops after 0.5 s, then coefficient of friction will be nearly
View Solution
Knowledge Check
If a block moving up an inclined plane at 30∘ with a velocity of 5 m/s , stops after 0⋅5 s , then coefficient of friction will be nearly
A0.5B0.6C0.9D1.1A block is projected upwards with a velocity of 5 m/s from the bottom of a rough inclined plane of inclination 30° with the horizontal. It stops after 0.5 s. What is the coefficient of friction ? (g=10m/s2)
A√3B1√3C√2D√5A marble block of mass 2 kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 10 s. Then the coefficient of friction is (g=10ms−2)
A0.02B0.03C0.06D0.01
A block slides down on inclined plane (angle of inclination 60∘ ) with an accelration g/2 Find the coefficient friction

View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View SolutionA body of mass 100g is sliding on a inclined plane with an inclination of 60∘. What is the frictional force experienced, if coeficient of friction is 1.7? (Take g=10m/s2)
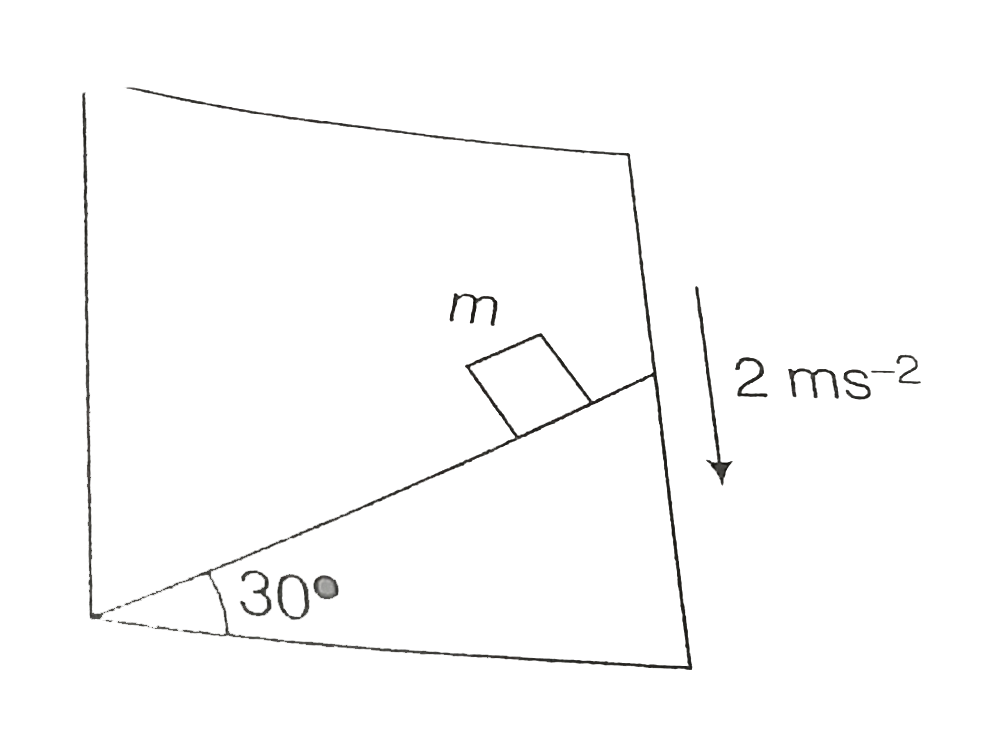
View SolutionA block of mass m is kept on an inclined plane of a lift moving down with acceleration of 2ms−1.What should be the coefficient of friction to let the block move down with constant velocity relative to lift.
View SolutionA particle is fired horizontally form an inclined plane of inclination 30∘ with horizontal with speed 50ms−1. If g=10ms−2 , the range measured along the incline is
View Solution
