The manager of a health club determines that the club's membership has increased at a rate of 16 percent per year for the past four years. The club currently has 42 members. If this trend continues, how many years will it take for the club's membership to exceed 100 membgers ?
4 years
5 years
6 years
7 years
The correct Answer is:C
To solve the problem of how many years it will take for the health club's membership to exceed 100 members given a current membership of 42 and an annual growth rate of 16%, we can use the concept of exponential growth.
1. Identify the Initial Conditions:
- Current membership (P) = 42 members
- Growth rate (r) = 16% = 0.16
- We want to find the number of years (t) it takes for the membership to exceed 100 members.
2. Set Up the Exponential Growth Formula:
The formula for exponential growth can be expressed as:
P(t)=P0⋅(1+r)t
where:
- P(t) is the future population (membership),
- P0 is the initial population (42 members),
- r is the growth rate (0.16),
- t is the number of years.
3. Substitute the Known Values:
We want to find t such that:
42⋅(1+0.16)t>100
This simplifies to:
42⋅(1.16)t>100
4. Divide Both Sides by 42:
(1.16)t>10042
Calculating the right side:
10042≈2.38
5. Take the Logarithm of Both Sides:
To solve for t, we take the logarithm:
log((1.16)t)>log(2.38)
Using the power rule of logarithms:
t⋅log(1.16)>log(2.38)
6. Solve for t:
t>log(2.38)log(1.16)
Now, calculating the logarithms:
- log(2.38)≈0.376
- log(1.16)≈0.063
Therefore:
t>0.3760.063≈5.95
7. Interpret the Result:
Since t must be a whole number (you can't have a fraction of a year in this context), we round up to the next whole number. Thus:
t=6
Conclusion:
It will take approximately 6 years for the club's membership to exceed 100 members.
- Current membership (P) = 42 members
- Growth rate (r) = 16% = 0.16
- We want to find the number of years (t) it takes for the membership to exceed 100 members.
The formula for exponential growth can be expressed as:
P(t)=P0⋅(1+r)t
where:
- P(t) is the future population (membership),
- P0 is the initial population (42 members),
- r is the growth rate (0.16),
- t is the number of years.
We want to find t such that:
42⋅(1+0.16)t>100
This simplifies to:
42⋅(1.16)t>100
(1.16)t>10042
Calculating the right side:
10042≈2.38
To solve for t, we take the logarithm:
log((1.16)t)>log(2.38)
Using the power rule of logarithms:
t⋅log(1.16)>log(2.38)
t>log(2.38)log(1.16)
Now, calculating the logarithms:
- log(2.38)≈0.376
- log(1.16)≈0.063
t>0.3760.063≈5.95
Since t must be a whole number (you can't have a fraction of a year in this context), we round up to the next whole number. Thus:
t=6
It will take approximately 6 years for the club's membership to exceed 100 members.
Topper's Solved these Questions
- BOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - EXPONENTS1videos
EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS
- BOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - POLYNOMIALS1videos
EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS
- BOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - RATIONAL EXPRESSIONS AND EQUATIONS1videos
EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS
- BOOK - KAPLANCHAPTER - ANSWERING SAT READING QUESTIONS EXERCISE - TRY ON YOUR OWN22videos
ANSWERING SAT READING QUESTIONS
- BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS1videos
FUNCTIONS
Similar Questions
The expression x(x3y2)−4 is equivalent to which of the following
05:18View SolutionIf −2x2+5x−8 is multiplied by 4x−9, what is the coefficient of x in the resulting polynomial?
01:57View Solution5y+7(y+4)2−5(y+4)
if the expression above the equal to −b(y+4)2, where b is a positive constatn and y≠−4, what is the value of b ?01:26View SolutionThis passage was adapted from an article titled "Quantum Computing, Where is it Going?" published in a science magazine in 2018. It discusses the background and potential of quantum computing.
Pharmaceutical companies dream of a time when their research and development process shifts from looking for illnesses whose symptoms can be ameliorated by a specific drug to choosing a diseaase and creating a frug to eradicate it.Quantum computing may be the key to that goal. The powerful modeling potential unlocked by quantum computing may also somedey be employed by autonomous vecicles to create a world free of traffic jams. With plausible applications in so many fields, it is worthwhile to learn a bit about how quantum computing works.
Any understanding of quantum computing begins with its most bgasic element, the qubit In classical computing, information is processed by the bit, the binary choice of zero or one. Qubits, on the other hand, allow for infinite superpositions between zero and one and thus can store and process exponentially more complicated values. imagine showing someone where you live on a globe by pointing only to either the North Pole or South Pole While you are likely closer to one pole than the other, you need additional information to represent your specific location. If, however, you could provide your home's lititude and longitude, it could be located without any additional information. The power of quantum computing lies in the ability to express precise information in a single qubit Quantum computing may help scientist and engineers overcome another barrie by reducing energy ouptup while increasing computational speed. The positive correlation between energy output and processing speed often causes classical computers to "run hot" while processing overwhelmine amounts of data. Along with their ability to store m,ultiple value simultaneously, qubits are able to process those values in parallel instead of serially. How does processing in parallel conserve energy ? Suppose you want to set the time on five separate alarm clocks spaced ten feet apart. You'd have to walk to each clock to change its time.
However if the clocks were connected such that changing the time on one immediatel7y adjusted the other four, you would expend less energy and increase processing speed. Therein lies the benefit of the quantum entanglement of qubits. While quantum computing has moved beyond the realm of the theoretical, significant barrieres still stand in he way of its practical application. One barrier is the diffcultly of confirming the results of quantum calculations. If quantum computing is used to solve problems that are impossible to solve with classical compting, is there a way to "check" the results? Scientists hope this paradox may soon be resolved. As a graduate student, Urmila Mahadev devoted over a decade to creating a verification process for quantum computing. The result is an interactive protocol, based on a type of cryptography called Learning With Errors (LWE), that is similar to "blind computing" used in cloud-computing to mask data while still performing calculations. Given current limatations, Mahadev's protocol remains purely theoretical, but rapid progress in quantum comuting combined with further refinement of the protocol will likely result in real world implementation within the next decade or two.
It is unlikely that early pioneers in the field, including Stephen Wiesner, Richard Feynman, and Paul Benioff, could have foreseen the rapid progress that has been made to date. In 1960, when Wiesner first developed conjugate coding with the goal of improving cryptography, his paper on the subject was rejected for publication because it contained logic far ahead of its time. Feynman proposed a basic quantum computing model at the 1981 First Conference on teh Physics of Computation. At that same conference, Benioff spoke on the ability of discreate mechanical processes to rase their own history and their application to Turing machines, a natural extension of Wiesner's earlier work. A year later, Benioff more clearly outlined the theoretical farmework of a quantum computer.
The dawn of the 21st century brought advancements at an even more impressive pace. The first 5-and 7-qubit nuclear magnetic resonance (NMR) computers were demonstrated in Munich, Germany, and Santa Fe, New Mexico, respectively. In 2006. researchers at Oxford were able to cage a qubit within a "buckyball," a buckminsterfullerene molecule, and maintain its state for a short time using precies, repated microwave pulses. The first company dedicated to quantum computing software, 1QB Information Technologies, was founded in 2012, and in 2018, Google announced the development of the 72-qubit Bristlecone chip designed to prove "quantum supremacy," the ability of quantum computers to solve problems beyond the reach of classical computing.
With progress in quantum computing accelerating, it seems inevitable that within a few decades, the general population will be as familiar with quantum computing as they now are with classical computing. At present, quantum computing is limited by the struggle to build a computer large enough to prove quantum supremacy, and the costs associated with quantum computing are prohibitive to all but the world's largest corporations and governmental institutions. Still classical computing overcame similar problems, so the future of quantum computing looks bright.
The primary purpose of the passage is to01:35View Solution
A certain cookie company sells several varieties of chocolate cookies, each with an add ingredient. The company sells the different varieties in differently sized boxes. The number of cookies per box and the profit per box for the different varieties is shown in the table above. The relationship between the number of cookies per box and the profit, in dollars, that the company makes per box can be represented by a linear function. Which of the following functions correctly represents the relationship ?08:00View SolutionThere are three clubs A,B,C in a town with 40,50,60 members respectively 10 people are members of all the three clubs,70 members belong to only one club.A member is randomly selected.Find the probability that he has membership of exactly two clubs
02:42View SolutionThe current membership of the Haryana Kisan Welfare Club is
01:49View SolutionIn a bank, principal increases continuously at a rate of 10% per year. In how many years Rs 1000, doubles itself ?
05:51View SolutionA school club includes only sophomores, jiniors, and seniors, in the ratio of 1:3:2. If the club has 42 members, how many seniors are in the club?
View Solution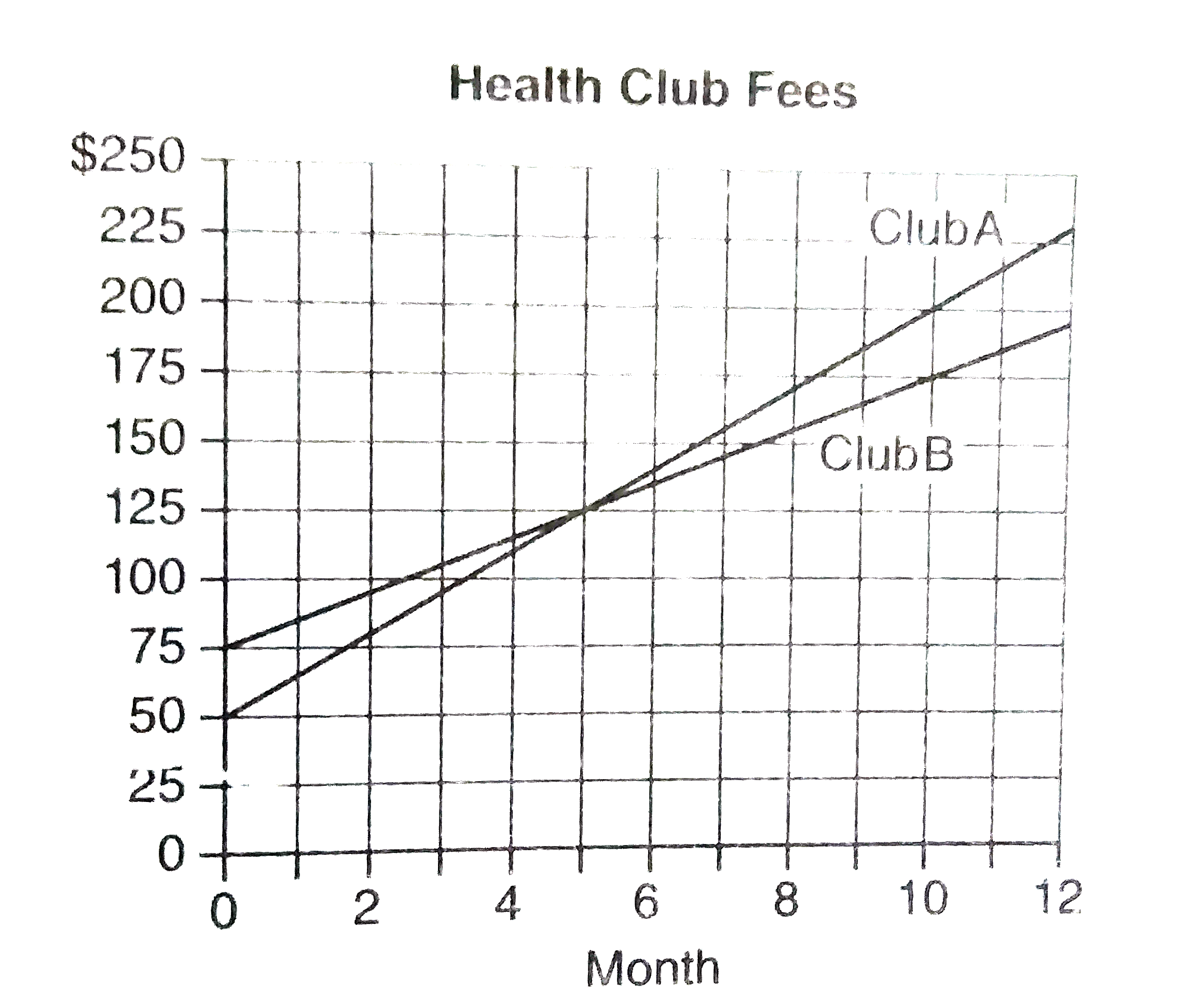
Two health clubs offer different membership plans. The accompanying graph represents the total yearly cost of belonging to Club a and Club B for one year. The yearly cost includes a membership fee plus a fixed monthly charge. By what amount does the monthly charge for Club A exceed the monthly charge for Club B?02:58View Solution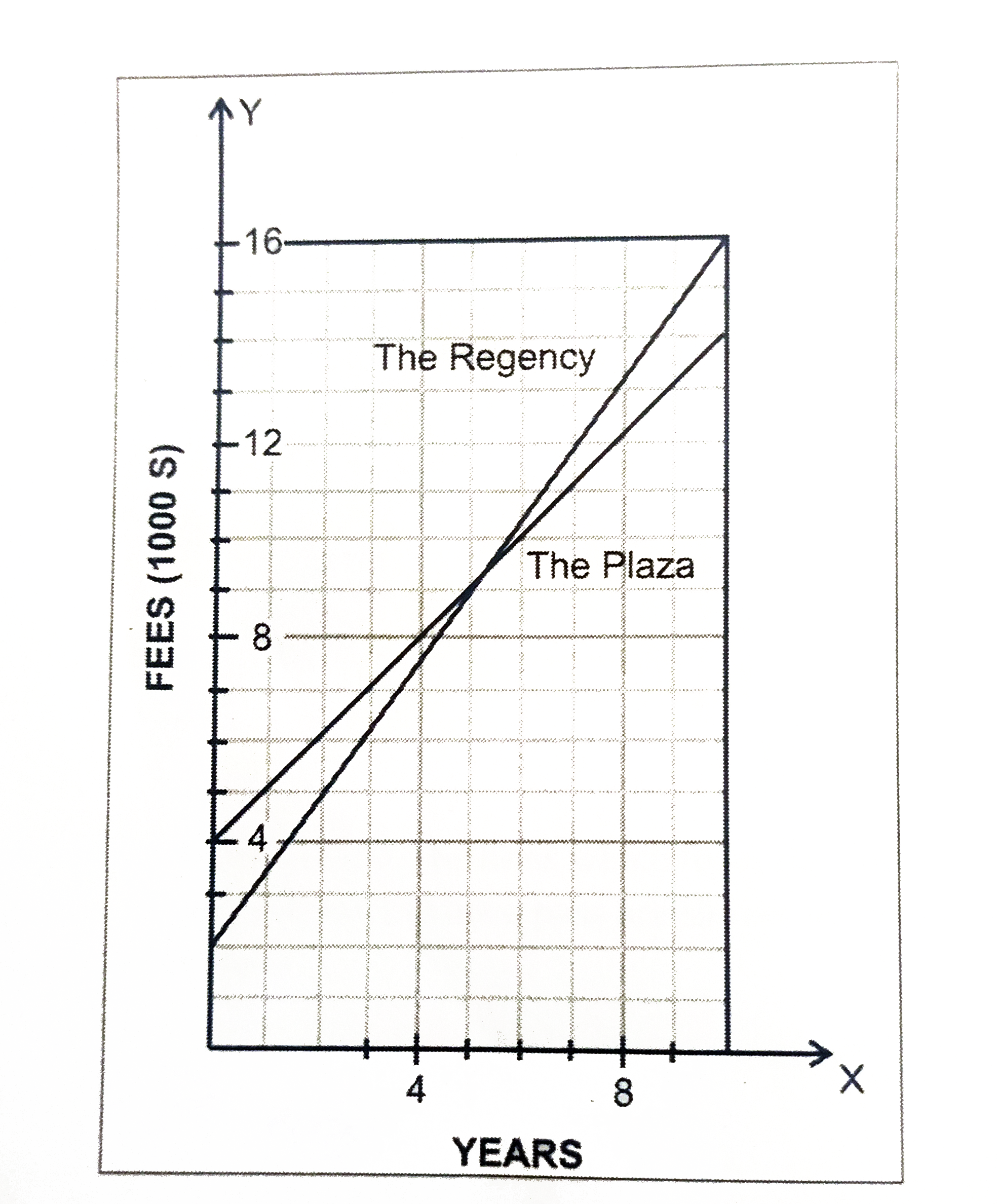
The membership plans of two health clubs, The Plaza and The Regency for ten years are shown in the graph below ( membership fees are in thousand dollars).For the intial registration , each club requires an upfornt payment of registration fees and every year thereafter one needs to pay a fixed annual membership fee. What is the difference between the annual charges of the two clubs ( in dollars ) ?07:01View SolutionIn a club, the average age of the members is 30 years, the average age of the male members is 34 years and that of the female members is 26 years. The percentage of the male members is
06:05View SolutionIn a bank, principal increases continuously at the rate of 5% per year. In how many years Rs 1000 double itself?
09:10View Solution_____ Sammy _____ Mary are in tech club this year.
02:59View SolutionThere were 2075 members enrolled in the club during last year. This year enrolment is decreased by 4%. How many members are enrolled during this year?
06:12View Solution

