For the function h defined above, c is constant and h(2)=10. what is the value of h(-2)?
The correct Answer is:C
To solve the problem step by step, we will follow the process outlined in the video transcript.
Step 1: Understand the function and the given condition
The function is defined as:
h(x)=cx2+18
We are given that h(2)=10.
Step 2: Substitute x=2 into the function
Using the given condition, we substitute x=2 into the function:
h(2)=c(22)+18
This simplifies to:
h(2)=c(4)+18
Step 3: Set up the equation using the given value of h(2)
Since we know that h(2)=10, we can set up the equation:
4c+18=10
Step 4: Solve for c
Now, we will isolate c:
1. Subtract 18 from both sides:
4c=10−18
4c=−8
2. Divide both sides by 4:
c=−84
c=−2
Step 5: Rewrite the function with the value of c
Now that we have found c, we can rewrite the function:
h(x)=−2x2+18
Step 6: Calculate h(−2)
Next, we need to find h(−2):
h(−2)=−2(−2)2+18
This simplifies to:
h(−2)=−2(4)+18
h(−2)=−8+18
h(−2)=10
Final Answer
Thus, the value of h(−2) is:
10
---
The function is defined as:
h(x)=cx2+18
We are given that h(2)=10.
Using the given condition, we substitute x=2 into the function:
h(2)=c(22)+18
This simplifies to:
h(2)=c(4)+18
Since we know that h(2)=10, we can set up the equation:
4c+18=10
Now, we will isolate c:
1. Subtract 18 from both sides:
4c=10−18
4c=−8
2. Divide both sides by 4:
c=−84
c=−2
Now that we have found c, we can rewrite the function:
h(x)=−2x2+18
Next, we need to find h(−2):
h(−2)=−2(−2)2+18
This simplifies to:
h(−2)=−2(4)+18
h(−2)=−8+18
h(−2)=10
Thus, the value of h(−2) is:
10
Topper's Solved these Questions
- ALEGBRABOOK - PRINCETONCHAPTER - ALEGBRAEXERCISE - QUICK QUIZ #6
3 Videos
- ALEGBRABOOK - PRINCETONCHAPTER - ALEGBRAEXERCISE - QUICK QUIZ #4
3 Videos
- ADVANCED ARITHMETICBOOK - PRINCETONCHAPTER - ADVANCED ARITHMETICEXERCISE - Examples
25 Videos
- ALGEBRA: CRACKING THE SYSTEMBOOK - PRINCETONCHAPTER - ALGEBRA: CRACKING THE SYSTEMEXERCISE - Algebra Drill 2: Calculator-Permitted Section
6 Videos
Similar Questions
Knowledge Check
h(x)=−2(x2−5x+3)+7(c−x)
In the polynomial h(x) defined above, c is a constant. If h(x) is divisible by x, what is the value of c?A−67B0C67D6h(x)=2x
The function h is defined above. What is h(5) − h( 3) ?A2B4C24D28g(x)=2x-1
h(x)=1-g(x)
The functions g and h are defined above. What is the value of h(0) ?A−2B0C1D2
The figure above shows the graph of function h. If function f is defined by f(x)=h(2x)+1, what is the value of f(−1)?
View Solutiong(x)=xx−2andh(x)=√9−x
Given of the following defined above, what is the value of (g∘h)(5)?
View SolutionIf function h is defined by h(x)=ax2−7andh(−3)=29, what is h(12)?
View Solution
Several values for the functions g (x) and h (x) are shown in the table above. What is the value of g(h(3)) ?
View Solution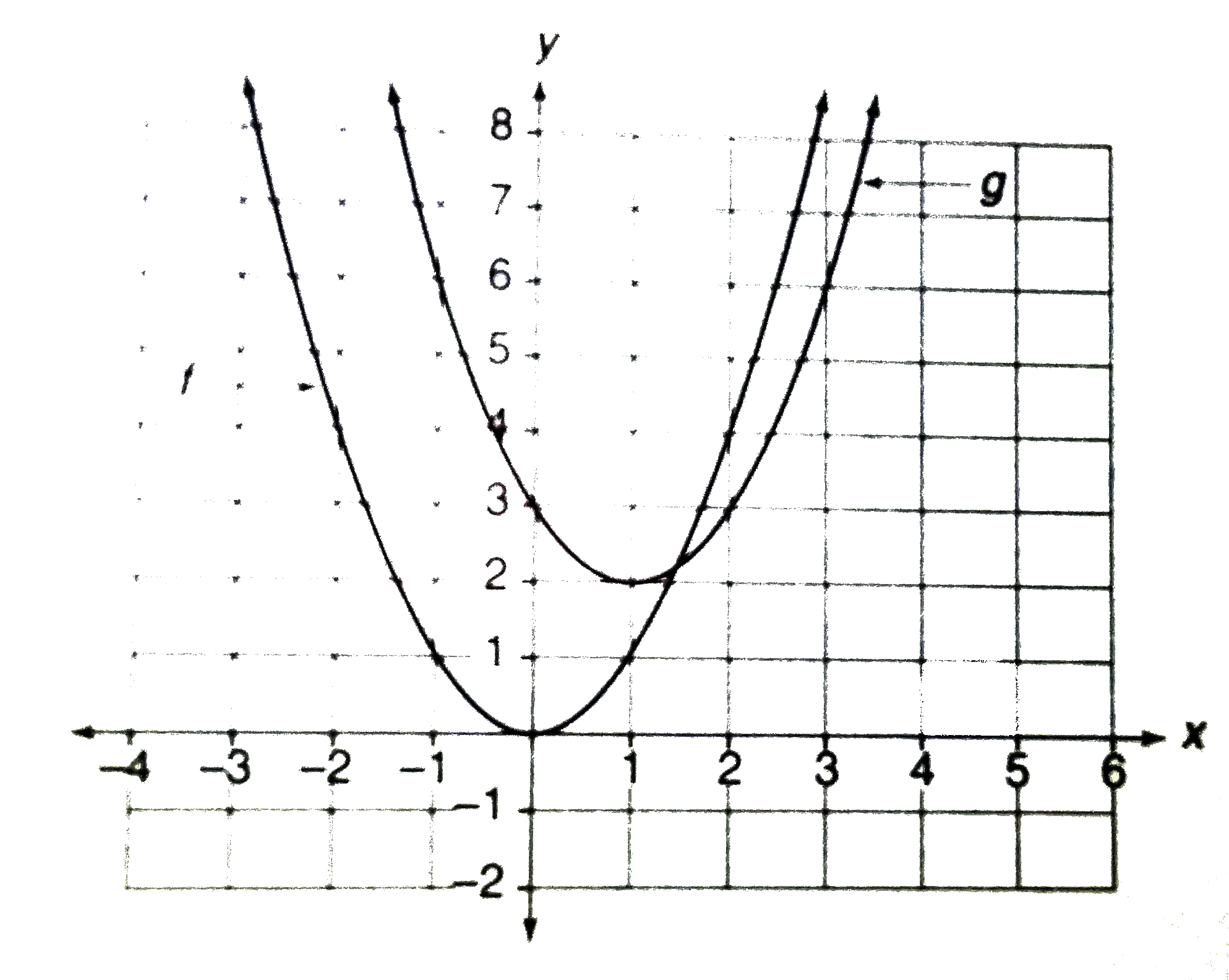
The accompanying figure shows the graphs of functions f and g. If f is defined by f(x)=x2 and g is defined by g(x)=f(x+h)+k, where h and k are constants, what is the value of h+k?
View Solution
