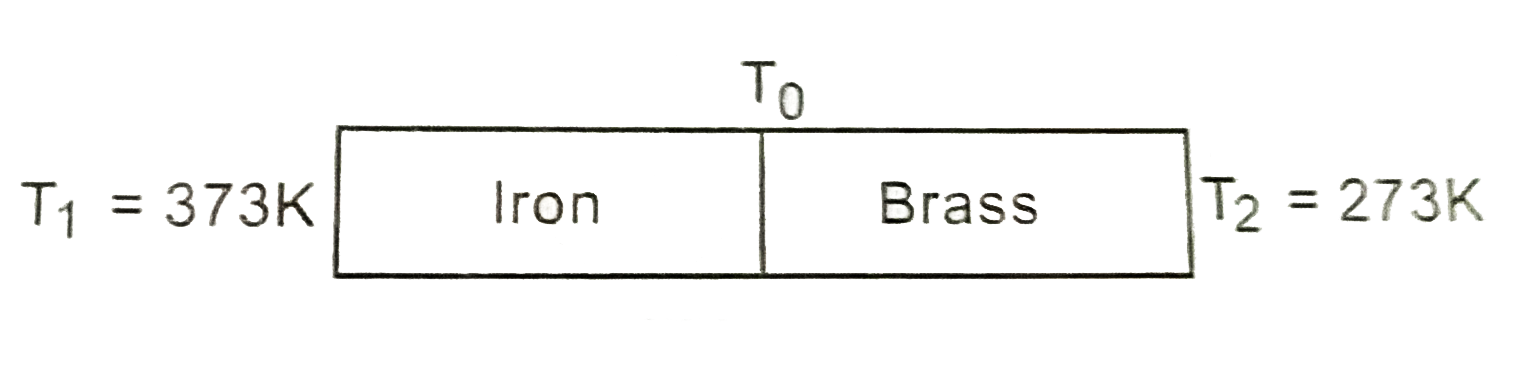
An iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
Given, Length L1=L2=L=0.1m
Area, A1=A2=A=0.02m2
Thermal conductivity, K1= 79 Wm−1K−1,K2=109Wm−1K−1
Temperature , T1=373 K and T2=273K
At steady state, heat transferred from any section of thermal conductor is same i.e. H1=H2=H
⇒(K1A1(T1−T0)L1=(K2A2(T0−T2)L2).......(ii)<br>ForA_(1)=A_(2)=AandL_(1) = L_(2) = L,Eq.(i)becomesK_(1)(T_(1)-T_(0)) = K_(2)(T_(0)-T_(2)) rArrT_(0)=(K_(1)T_(1)+K_(2)T_(2))/(K_(1)+K_(2))<br>Therefore,heatcurrentthroughother¯¯¯¯¯¯<br>H= (K_(1)A(T_(1)-T_(0)))/L=(K_(2)A(T_(0)-T_(2)))/L = A(T_(1)-T_(2))/(L(1/K_(1)+1/K_(2)))<br>Now,heatcurrentthroughcomposite¯of≤n>hL_(1)+L_(2) = 2Land≡a≤ntthermalconductivityK^('),canbegivenby<br>H^(') = (K^(')A(T_(1)-T_(2)))/(2L) = H rArrK=(2K_(1)K_(2))/(K_(1)+K_(2))<br>(i)So,thetemperatureofthejunctionoftwo¯sis<br>T0=K1T1+K2K2K1+K2
=79Wm−1×373K+109Wm−1K−1×273K79Wm−1K−1+109Wm−1K−1
91.6Wm−1K−1
iii) Heat current through the composite bar
H′=H=(K′AT1−T22L
(91.6 Wm^(-1)K^(-1) xx 0.002m^(3) xx (373 -273)K)/(2 xx 0.1)m
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.110videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.210videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective14videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
Similar Questions
The outer face of a rectangular slab of equal thickness of iron and brass are maintained at 100∘C and 0∘C, respectively. Find the temperature of the interface. The conductivities of iron and brass are 14 and 126Wm−1K−1 respectively.
View SolutionEqual volume of 0.1MH2CO3(Ka1=10−7,Ka2=10−11) and 0.1MH2S(Ka1=10−7,Ka2=10−14) are mixed together. Calculate value of pOH−pH for resulting solution.
View Solution
Knowledge Check
- Question 1 - Select One
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1 - Question 2 - Select One
If L1=(2.02±0.01)m and L2=(1.02±0.01)m then L1+2L2 is (in m)
A4.06±0.02B4.06±0.03C4.06±0.005D4.065±0.01 - Question 3 - Select One
Two bars of thermal conductivities K and 3K and lengths 1cm and 2cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite bar is 0∘C and K2/l respectively (see figure), then the temperature ϕ of the interface is
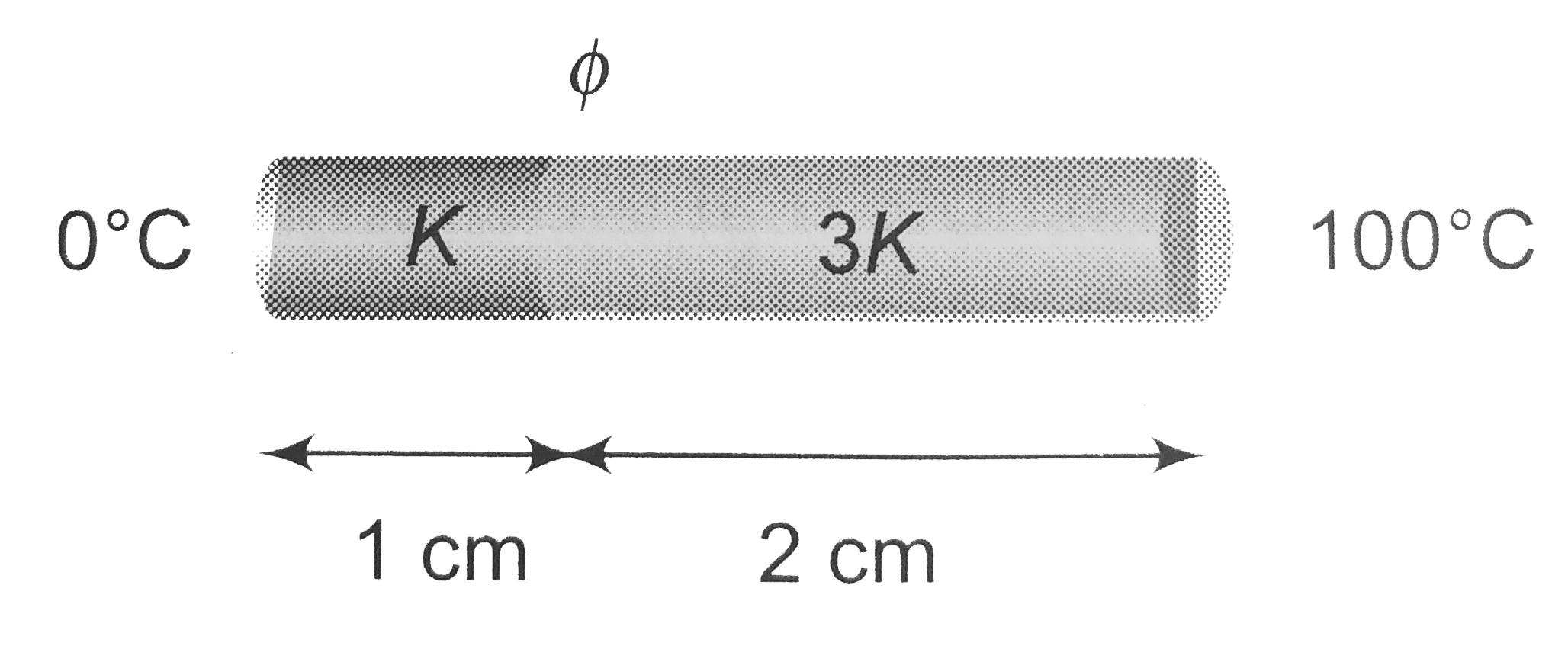 A50∘CB1003.∘CC60∘CD2003.∘C
A50∘CB1003.∘CC60∘CD2003.∘C
A steel bar 10.0 cm long is welded end to end to a copper bae 20.0 cm long. Both bars are insulated perfectly on their sides . Each bar has a separate cross-section, 2.00 cm on a side . The free end of the steel bar is maintained at 100∘C by placing it in contact with ice . find the temperature at the junction of the two bars and the total rate of heat flow . thermal conductivity of steel =50.2Wm−1K−1.thermal conductivity of copper =385Wm−1K−1.
View SolutionA bar of copper of length 75 cm and a bar of steel of length 125 cm are joined together end to end . Both are of circular cross - section with diameter 2 cm . The free ends of the copper and steel bars are maintained at 100∘C and 0∘C respectively . The surface of the bars are thermally insulted . What is the temperature of the copper - steel junction ? What is the heat transmitted per unit time across the junction ? Thermal conductivty of copper 9.2×10−2kcalm−1∘C−1s−1 and that of steel is 1.1×10−2kcalm−1s−1(∘)C−1.
View SolutionA bar of length 1 m is supported at its two ends. The breadth and depth of the bar are 5 cm and 0.5 cm., respectively , A body of mass 0.1 is suspended at the centre of the bar. Calculate the depression produced in the bar.
View SolutionTwo bars, A and B, each of length 2.0 m and cross-sectional area 10m2, are placed and to end as shown in the figure.
The thermal conductivities of the bars are kA=339(J/s.m.K) and kB=837J/(s.m.K), respectively. The left end of bar A is maintained at 373 K while the right end of B is maintained at 273 K

Wha tis the temperature at the interface between A and B?View SolutionCalculate Q and w for the isothermal reversible expansion of one mole an ideal gas from an initial pressure of 1.0 bar to a final pressure of 0.1 bar at a constant temperature of 273 K respectively.
View Solution

