A bar of length 1 m is supported at its two ends. The breadth and depth of the bar are 5 cm and 0.5 cm., respectively , A body of mass 0.1 is suspended at the centre of the bar. Calculate the depression produced in the bar.
Data : L = 1 m, b = 5 cm = 5×10−2m.d=0.5cm=5×10−3 m
M=0.1kg,Y=2×1011N/m2
Load , W = Mg = 0.1×9.8=0.98N
The depression (sag) produced in the bar.
δ=W4by(ld)3=0.984(5×10−2)(2×1011).(15×10−3)3
=0.984×1016.(2×102)3=0.98×8×1064×1010=1.96×10−4m=0.196mm
Topper's Solved these Questions
- SOLVED PROBLEMS - I BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS - I EXERCISE - WAVE MOTION
11 Videos
- SOLVED PROBLEMS - I BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS - I EXERCISE - STATIONARY WAVES
17 Videos
- SOLVED PROBLEMS - I BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS - I EXERCISE - ROTATIONAL MOTION
26 Videos
- SHORT ANSWER QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SHORT ANSWER QUESTIONSEXERCISE - Assignments
3 Videos
- SOLVED PROBLEMS-II BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS-II EXERCISE - Assignments
5 Videos
Similar Questions
A uniform bar AB of length 6a has been placed on a horizontal smooth table of width 5 a as shown in the figure. Length 2a of the bar is overhanging. Mass of the bar is 4m. An insect of mass m is sitting at the end A of the bar. The insect walks along the length of the bar to reach its other end B.
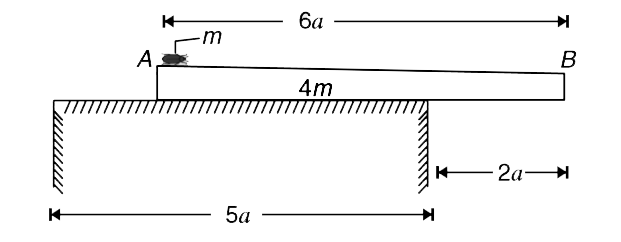
(a) Will the bar topple when the insect reaches end B of the bar ?
(b) After the insect reaches at B, another insect of mass M lands on the end A of the bar. Find the largest value of M which will not topple the bar.
View SolutionA thin uniform bar lies on a frictionless horizontal surface and is free to move in any way on the surface. Its mass is 0.16 kg and lengths is √3m. Two particles, each of mass 0.08kg, are moving on the same surface and towards the bar in a direction perpendicular to the bar, one with a velocity of 10ms−1 and the other with 6ms−1, as shown in fig. The first particle strikes the bar at point A and the other at point B. Points A and B are at a distance 0.5 m from the centre of the bar. The particles strike the bar at same instant of time and stick to the bar on collision. Calculate the loss of kinetic energy of the system in the above collision process.

View Solution
Knowledge Check
A steel bar AB of mass 10 kg and length 1 m is kept horizontal by supporting it at the two ends. Two weights of 4 kg and 6 kg are suspended from points of the bar at distances 30 cm and 80 cm respectively from the end A. The reaction at the end A is
A107.8 NB97.8 NC88.2 ND78.2 NA rectangular bar 2 cm in breadth, 1cm in depth and 100 cm in length is supported at its ends and a load of 2kg is applied at its middle. If young's modulus of the material of the bar is 20×1011 dyne / cm−2, the depression in the bar is
A0.2450 cmB0.3675C0.1225 cmD0.98In a bar graph, length of a bar is 6.4 cm and it represents 256 units. Find the number of units represented by a bar of length 5.3 cm.
A228B196C212D224
A non-uniform bar weight W and length L is suspended by two strings of negligible weight as shown in figure. The angles made by the strings with the vertical are θ1 and θ2 respectively. The distance d of the centre of gravity of the bar from its left end is
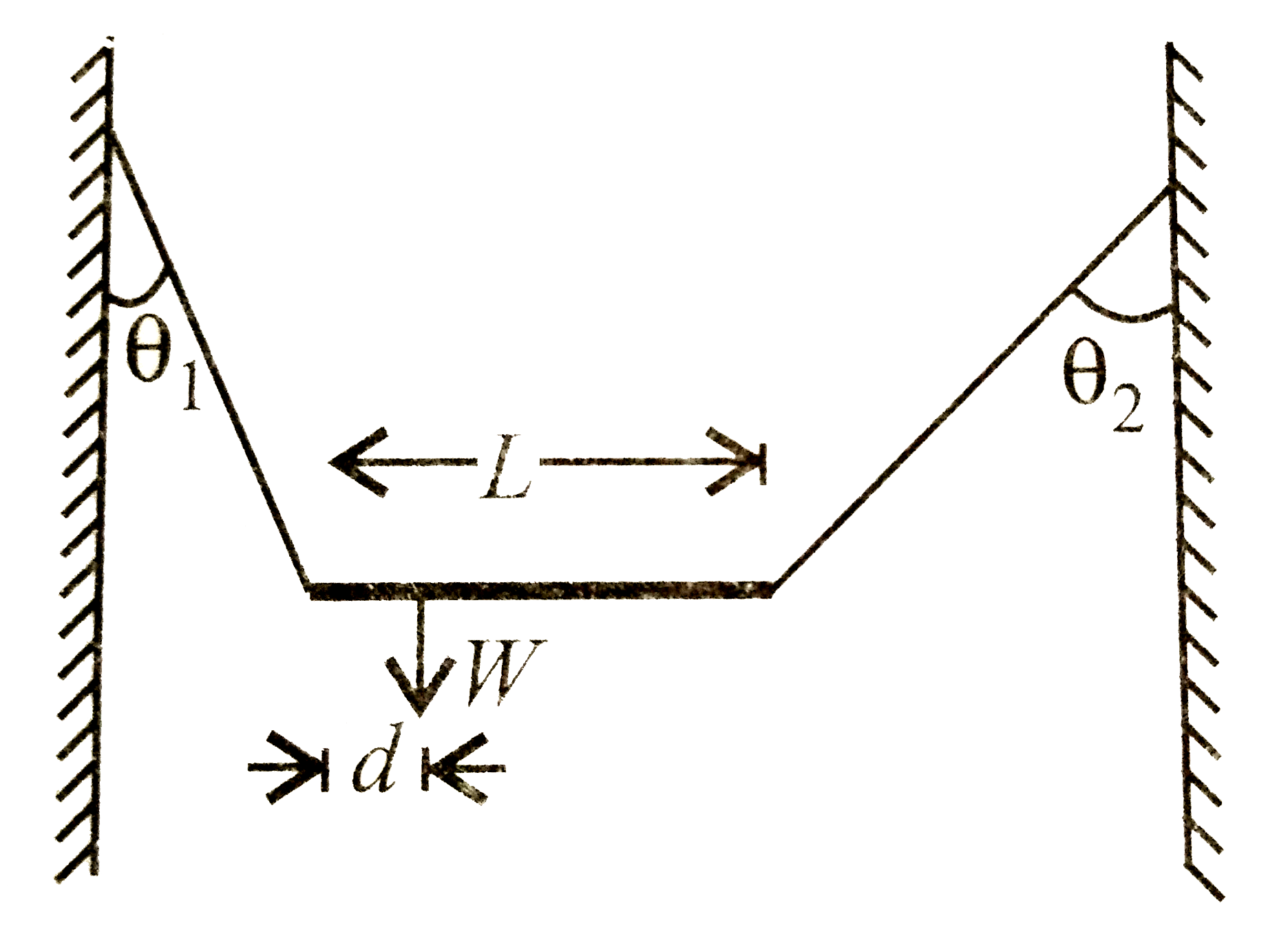
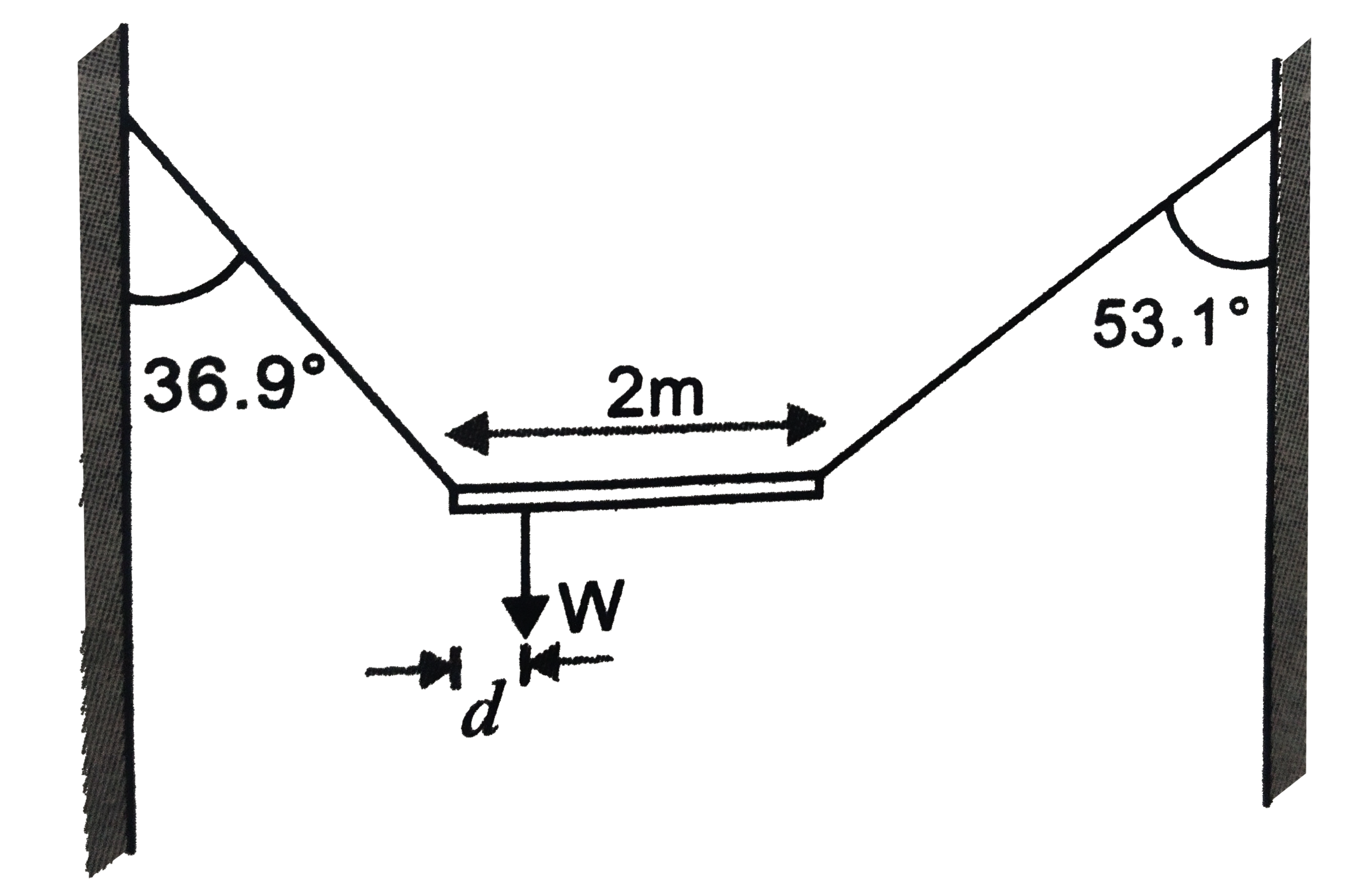
View SolutionA non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9∘and53.1∘ respectively. The bar is 2m long. Calculate the distance d of the centre of gravity of the bar from its left end.
View SolutionA bar graph is draph is drawn to the scale of 1cm=k units.
The length of the bar representing 260 units is 5.2 cm. Find the value of k.
View SolutionA bar graph is drawn to the scale of 1 cm = k units. The length of the bar representing a quantity 405 units is 5.4 cm. Find k.
View SolutionIn a bar graph, the length of a bar is 5.5 cm and it represents 450 units. Find the number of units represents by a bar of length 2.2 cm.
View Solution
